서포트 벡터 머신 Support Vector Machine, SVM
서포트 벡터 머신 Support Vector Machine, SVM 은 서포트 벡터를 기준으로 클래스를 판별한다.
아래 그림의 각 클래스는 2개의 데이터 포인트로 구성, 데이터 포인터들을 클래스를 기준으로 구분하는 직선들을 생성할 수 있다.
이 중 서포트 벡터 머신은 중심선과 경계선을 이용해 데이터를 구분한다. 그 경계선을 서포트 벡터라고 한다.
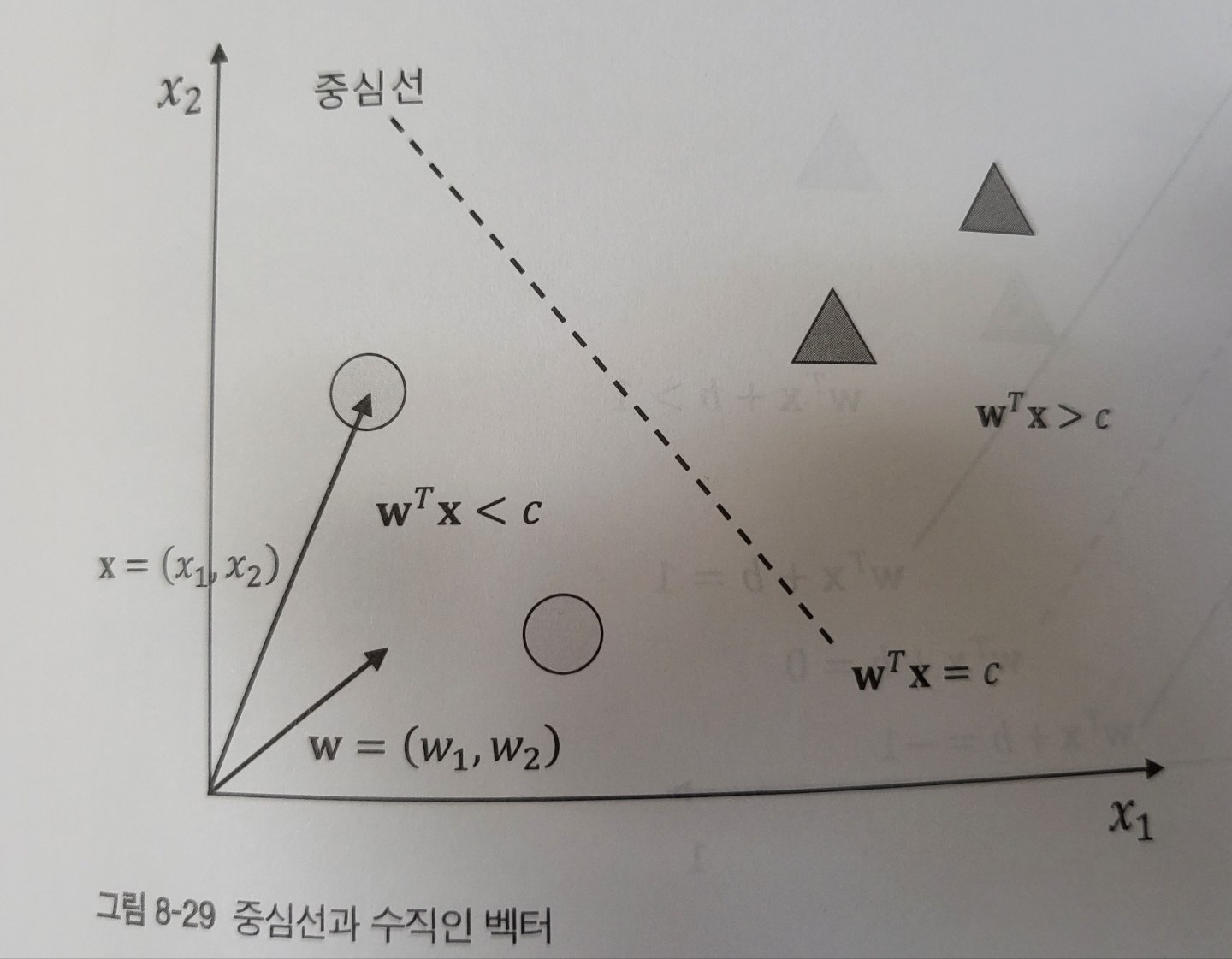
먼저 중심선을 그리는 방법을 알아본다.그러기 위해선 중심선에 수직인 벡터 w를 구하는 것이 중요하다.
중심선에 수직인 벡터 w 와 데이터 포인트 x 를 내적했을 때, 내적값 c가 되는 지점이 중심선이 되고 이는 Wx=c 라고 표현할 수 있다. 내적값 c가 되는 지점인 중심선을 기준으로 영역을 나눌 수 있다.
위 그림과 같이 데이터 공간을 내적값이 c보다 큰 영역과 c보다 작은 영역으로 각각 나누면 중심선 윗부분과 아랫부분으로 나눌 수 있다는 것을 알 수 있다.
중심선을 변환, 중심선 Wx=c 에서 우변을 0으로 변환시킨다. c를 좌변으로 이항시키고 치완하여 중심선을 W^Tx + b=0 이라고 표현할 수 있다.
p차원으로 일반화시키면 (x1, y1), (x2, y2),...,(xn, yn) 이 존재할 때, xi∈R^p 이며, 타깃 데이터는 -1 또는 1에 속한다.
이 때, 아래와 같은 초평면을 가정한다. 아래 수식이 데이터 클래스를 구분하는 초평면이다.
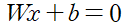
가중치 wi 는 wi∈R^p 이다. 이를 이용해 중심선과 경계선을 다시 나타내면 아래와 같다.

위 그림에서 중심선과 거리를 편의상으로 1로 설정, 각 영역을 나타내는 식을 간단히 나타내면 다음과 같다. 다음 식에서 sign 은 부호를 의미한다.
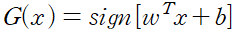
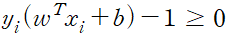
서포트 벡터 머신에서는 마진을 최대화하는 것이 목표이다. 마진이란 서포트 벡터 간 너비를 의미한다. 마진은 어떻게 구할 수 있을까?

그림과 같이 중심선에 수직인 벡터 w와 서포트 벡터에 걸쳐 있는 데이터 x1과 x2를 이용하면 마진을 구할 수 있다.
서포트 벡터 간 마진을 구하는 식은 아래와 같다.

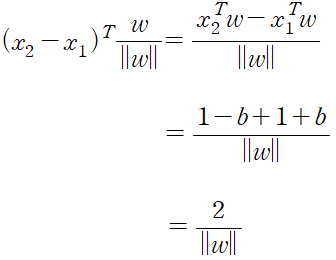
마진이 2/||w|| 라는 말은 서포트 벡터 머신의 마진이 w(중심선에 수직인 직선)에 의해 결정된다는 의미다.
서포트 벡터 머신의 목적은 마진의 최대화므로 앞서 구한 마진을 최대화, 마진을 2M 으로 표시
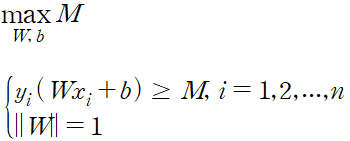
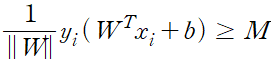
위와 같이 쓰면 w의 크기가 1로 변경됨으로써 더 이상 ||w||=1 제약식을 사용하지 않아도 된다.
양변에 ||w|| 의 곱

위 식에서 M = 1/||w|| 이라는 사실을 이용하여 제약식을 변경한다.
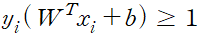
정리한 제약식을 적용하면 서포트 벡터 머신의 최적화 식을 아래와 같이 표현할 수 있다.
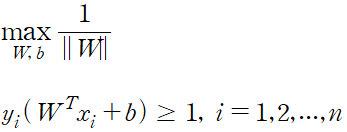
위 식에서의 변경

목적 함수와 제약식을 라그랑주 프리멀 함수 형태로 표현
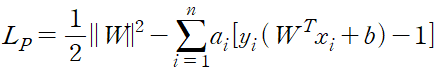
이 식의 최적값을 구하기 위해 w, b에 대해 미분 시행


위에서 구한 편미분 결괏값을 라그랑주 프리멀 함수에 대입해 라그랑주 듀얼 함수를 구할 수 있다.
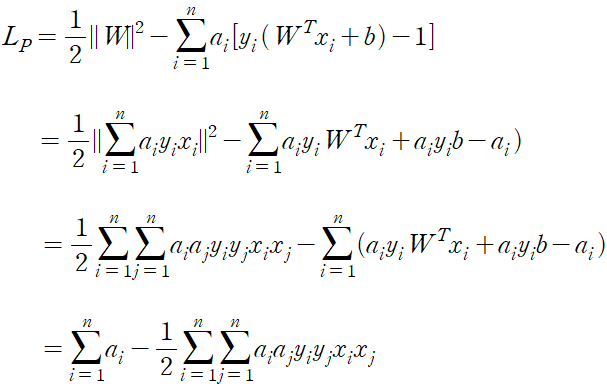
라그랑주 프리멀 함수와 듀얼 함수를 모두 만족하는 최적값임을 보이기 위해서는 KKT 조건을 만족하므로 아래 식이 성립해야 한다.

위 식이 0인 이유는 앞서 라그랑주 듀얼 함수에서 ai>=0 임을 알 수 있다. 만약 ai>0 이라면 xi 가 서포트 벡터에 걸쳐 존재한다는 의미이므로 1이 되어 위 식은 0을 만족하고, 만약 >1 이라면 xi 가 경계선에 존재하지 않으므로 제약 조건이 발동되지 않아 ai=0 이 성립된다.