경사 하강법과 미적분

적분의 이해

위 식의 의미는 “x를 a부터 b까지 변화시키면서 f(x)에 dx를 곱한 것을 전부 합쳐라”라는 의미.

적분기호는 Intergral 이라고 읽는데 영어의 S의 모양이다. Sum의 S를 길게 늘어뜨린 기호이다.

다음 f(x)dx는 f(x)에다 dx를 곱하라는 말로 함수 그래프를 통해 살펴보면

함수값 f(x)는 y = f(x) 그래프에서 x가 x일 때의 y값, 즉, 빨간색 선의 높이(길이)이다.

dx는 미분에서의 dx와 동일한 의미로 x의 순간적인 변화량이다. 이와 관계된 표현으로 △x가 있는데 구간에서의 x의 변화량으로 만일, x가 x1에서 x2로 값이 변했다면 △x = x2 - x1 이다.

dx는 △x를 무한히 작은 값으로 보낸 극한에서의 개념, f(x)dx가 의미하는 것은 빨간색 선의 넓이이다.

적분 식을 다시 보면, x를 a부터 b까지 변화시키면서 f(x)에다가 dx를 곱해서 합친다라는 의미로 위 함수의 면적을 구하는 식을 의미한다.

미분의 이해

적분의 반대말이 미분이다. 적분이 쌓는 것이라면 미분은 미세하게 쪼개는 것으로 순간변화율이라고도 한다.

우선, 변화율이란 무엇에 대한 변화율으로 변화율을 말하기 위해선 변화율의 기준이 있어야 한다.

위 식이 미분에 대한 기본적인 식으로 함수의 변화율을 같이 보면,

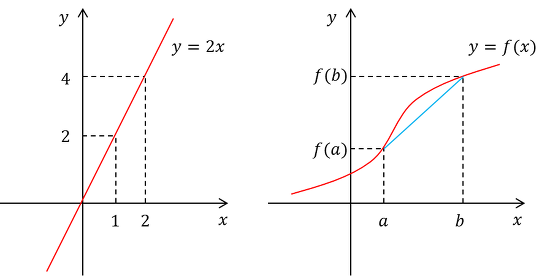
먼저 왼쪽 그림은 기울기가 2인 직선으로 dy/dx = 2이다. y변화량이 x변화량의 2배라는 의미로 x가 1 증가할 때마다 y가 2 씩 증가한다는 의미

오른쪽 곡션 y = f(x)의 경우 변화율이 어떻게 될까? 직선처럼 변화율이 항상 일정하지 않고 곡선의 경우 변화율이 변화한다. 순간 순간의 변화율은 계속 변하지만, 어떤 구간에서의 평균적인 변화율을 정의할 수 있다.

여기서 평균변화율 개념이 나온다 .함수 f(x)의 구간 [a,b] 에서의 평균변화율은 다음과 같이 주어진다.

위 평균 변화율 예에서 x는 a에서 b로 변했으므로 x의 변화량 △x는 △x = b -a이다.

이제 미분의 원래 정의인 순간 변화율에 대해 알아보면,

위 곡선 예에서 구간의 평균 변화율이 아닌 모든 x점에서의 순간 변화율을 구하는 것이 목적이다. 즉 곡선위의 한 점, 한 점에서의 변화율을 구하고 싶은 것이다. 곡선상의 어떤 한 점을 무한히 부분적으로 직선이 된다. 이 직선의 기울기가 바로 해당 점에서의 순간 변화율이다.

위 곡선 예에서 x = a에서의 순간 변화율 f'(a)는 다음과 같이 구할 수 있다.

x = a 의 한 점에서가 아닌 모든 점에서의 순간 변화율을 구하고 싶으면 x를 특정 값으로 국한시키지 않고 x 자체에 대해 일반적으로 순간 변화율을 구하면 된다.

이러한 미분은 어떤 함수가 있을 때, 이 함수가 어떤 변수에 의해 어떻게 영향을 받는지 분석하는 가장 핵심적인 도구로 사용된다.

머신러닝에서의 미분, 경사 하강법

머신러닝의 목표는 새로운 값에 대한 예측이다. 예를 들어 x, y의 두 개의 값을 가지는 데이터가 있을 때 우리는 이 데이터를 가장 잘 설명할 수 있는 함수 f(x)를 구할 수 있다.

위 그래프의 x가 키, y가 몸무게라고 생각해보자. 우리는 5명의 키와 몸무게를 통해 이 데이터를 설명할 수 있는 함수 f(x)를 구하고 싶어한다.

f(x) = ax + b 형태의 1차 함수를 구한다고 할 때 학습을 통해 a, b 값을 구해야 하고, 최적의 a, b 값을 구하는 방법으로 임의의 a, b로 만들어진 함수 f(x)와 데이터 사이의 거리를 이용한다.

그래프를 확대한 모습으로, 데이터와 함수 f(x)의 수직선의 거리를 구하고 이들의 합이 최소가 되는 a, b를 찾아야 한다.

변화하는 a, b값에 대해 데이터들과 함수 f(x)와의 거리의 합이 최소가 되는 값을 찾기 위해 미분이 사용

A(거리의 합)의 B(a, b의 값)에 대한 변화율을 구하는 것

이 변화율이 감소하여 0에 가까운 지점을 탐색한다. 이 지점이 거리의 합이 최소가 되는 a,b의 값이다.

파라미터 (a,b)에 대한 거리의 합 그래프

해당 그래프의 최솟값은 변화율, 기울기(미분값)가 0에 가까워지는 지점이다.

https://darkpgmr.tistory.com/45

미분 적분 제대로 알자

해당 블로그의 글 참고