1.6 고윳값과 고유벡터
A 의 고유벡터는 A 에 그 벡터들을 곱해도 방향이 변하지 않는다는 성질을 가진다. 결과인 Ax 는 대입한 벡터 x 와 같은 선상에 있다.
x = A 의 고유벡터, lamda = A 의 고윳값, Ax = lamda x
고유벡터 x 는 단지 고윳값인 lamda 를 곱한 형태이다. 다시 A 를 곱한 A^2 의 고유벡터 또한 x 임을 알 수 있다.
고유벡터는 A에 의존하는 특별한 벡터이다. 대부분의 n*n 행렬에는 n 개의 독립인 고유벡터 x1 ~ xn 과 그에 대응하는 n 개의 서로 다른 고윳값 lamda 1 ~ lamda n 이 있다. 이 경우 모든 n 차원 벡터 v 는 다음과 같이 그 고유벡터들의 일차결합으로 표현된다.
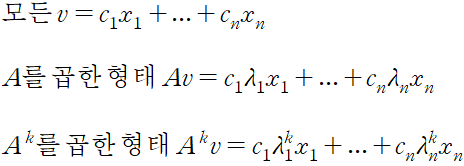
고윳값과 고유벡터가 얼마나 유용한지 알 수 있으며, 이를 통해 행렬을 꿰뚫어 볼 수 있다. 만약 |lamda 1|>1 이라면 성분 은 n 이 커짐에 따라 계속 커질 것이다. 반대의 경우 점차 사라질 것
예제 1
S = (2,1)(1,2) 의 고유벡터는 다음과 같다.
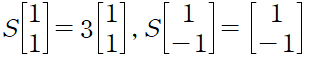
lamda_1 = 3, lamda_2 = 1 이다. S^k 는 3^k 처럼 점점 커질 것이다.
고윳값과 고유벡터에 대하여 다음과 같은 네 가지 성질이 성립한다.
- S 의 대각합 : 합 lamda 1 + lamda 2 = 3+1 은 대각성분의 합 2+2=4 과 ㅏㄱㅌ다.
- 행렬식 : 곱 lamda 1 * lamda 2 은 행렬식 4 - 1 과 같다.
- 실수 고윳값 : 대칭행렬 S = S^T 의 고윳값은 항상 실수이다.
- 직교 고유벡터 : 람다값이 다르면 x_1 * x_2 = 0 이다. 여기서 (1,1)·(1,-1) = 0 이다.
대칭행렬 S 는 실수와 비슷하다. 직교행렬 Q 는 크기가 1인 복소수와 비슷하다. Q 의 거듭제곱은 크거나 작아지지 않는다. 왜냐하면 모두 직교행렬이기 때문이다.
예제 2
회전행렬 Q = (0,-1)(1,0) 의 고윳값은 허수 i, -i 이다.
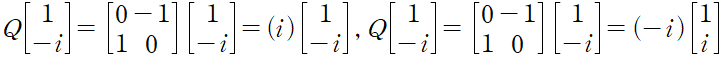
lamda 1 + lamda 2 = i - i 는 Q 의 주대각성분의 합 0+0 과 같다. 그리고 lamda 1 * lamda 2 = i * -i 는 Q 의 행렬식 1 과 같다. Q 의 고유벡터가 복소벡터인 경우에도 내적을 이용하면 여전히 직교함을 알 수 있다. x_1 의 모든 i 를 -i 로 바꾸자. 이렇게 해서 켤레복소수를 얻을 수 있다.
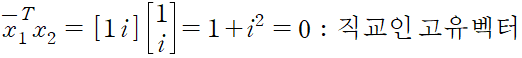
- A + B 의 고윳값은 일반적으로 lamda(A) 와 lamda(B) 의 합과 같지 않다.
- AB 의 고윳값은 일반적으로 lamda(A) 와 lamda(B) 의 곱과 같지 않다.
- 중복된 고윳값 lamda_1 = lamda_2 는 일차독립인 2개의 고유벡터와 있을 수도 없을 수도 있다.
- 실수 행렬 A 의 고유벡터가 직교하는 것과 A^TA = AA^T 인 것은 동치이다.