1.6.3 행렬의 대각화

A 가 일차독립인 n 개의 고유벡터를 가진다고 가정하자. 그 고유벡터 x_1,...,x_n 으로 가역행렬 X 를 만들자. 그러면 곱 AX 를 열별로 곱하여 lamda_1 x_1,...,lamda_n x_n 을 얻는다. 중요한 사실은 이 행렬이 X 와 ∀ 의 곱으로 분해된다는 것이다.

고윳값 행렬 A 의 lamda 들은 X 의 열에 곱해지므로, ∀ 는 X 의 오른쪽에 놓인다. 방정식 AX = X∀ 에서 A = X∀X^-1 임을 알 수 있다. 만약 고윳값과 고유벡터를 안다면 행렬 A 를 알 수 있으며, A 의 거듭제곱을 계산할 수 있다.

∀ = 대각 고윳값 행렬, X = 가역인 고유벡터 행렬 A = X∀X^-1, A^2 = X∀^2X^-1

예제 3의 A를 A = X∀X^-1 형태로 나타내면 다음과 같다.

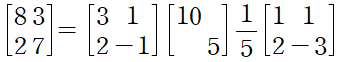
(고유벡터) * (lamda) * (좌고유벡터)

방정식 A^k = X∀^kX^-1 는 이미 알고 있는 다음 사실을 상기시킨다. A^k 의 고윳값은 lamda_1^k ~ lamda_n^k 이다.

A^k 의 고유벡터는 A 의 고유벡터와 같다. 다음은 A^kv 를 구하는 세 단계이다.

1. X^-1v 이것이 v = c_1x_1 + ... + c_nx_n 의 계수 c 들을 구할 수 있게 한다.
2. ∀^kX^-1v 이것이 c_1 lamda_1^k x_1 = c_1 lamda_1^k x_1 + ... + c_n lamda_n^k x_n 의 lamda 들을 구할 수 있게 한다.
3. X∀^kX^-1v 이것이 A^kv = c_1 lamda_1^k x_1 + ... + c_n lamda_n^k x_n 의 마지막 부분을 완성한다.

예제 4

예제 3 의 행렬을 10 으로 나누면 모든 고윳값은 10으로 나누어진다. 그러면 lamda_1 = 1 이고, lamda_2 = 1/2 이다. 이 경우 A 는 합이 1 인 양의 열을 포함하는 마르코프 행렬이다.

각 고유벡터는 개별적으로 살펴볼 수 있다. 고유벡터의 증가와 감소는 고윳값 lamda 에 의존한다. 전체 행렬 A 의 작용은 각 고유벡터에 대한 작용으로 나뉜다.