2. 딥러닝
데이터 처리 유닛의 층을 여러 개 쌓아 구조적이지 않은 데이터로부터 고수준 표현을 학습한다.
2.1 정형 데이터와 비정형 데이터
비정형 데이터는 특성의 열로 구성할 수 없는 데이터를 말한다. 데이터 하나하나는 거의 아무런 정보를 가지고 있지 않는다. 이러한 개별 데이터들이 모여 고수준 특성을 구성한다. 데이터의 구성 요소가 고차원 공간에서 의존성을 가지고 연결되어 있기 때문에 픽셀이나 문자를 독자적인 정보를 가진 특성으로 사용할 수 없다.
딥러닝 모델은 비정형 데이터로부터 직접 고수준 정보를 가진 특성을 만드는 방법을 스스로 학습할 수 있다.
2.2 심층 신경망
대부분의 딥러닝 시스템은 여러 개의 은닉 층을 쌓은 인공 신경망 Artificial Neural Network ANN, 이런 이유로 딥러닝이 심층 신경망과 거의 동의어, 여러 개의 층을 사용해서 입력 데이터에서 고수준 표현을 학습하는 어떤 시스템도 딥러닝의 한 형태이다.
심층 신경망은 층을 연속하여 쌓아 구성한다. 층은 유닛을 가지며, 이전 층의 유닛과 가중치로 연결된다. 밀집 층은 모든 유닛이 이전 층의 모든 유닛과 연결되는 것, 연속해서 쌓을수록 원본 입력의 복잡한 특징을 점점 잘 표현할 수 있다.
각 층의 가중치 조합을 찾는 과정을 훈련이라고 한다.
훈련 과정 동안 이미지의 배치가 네트워크에 전달되고 출력된 값을 정답과 비교, 예측 에러는 네트워크를 통해 거꾸로 전파되어 예측을 가장 많이 향상시킬 수 있는 방향으로 가중치를 조금씩 수정한다. 이 과정을 역전파 backpropagation 라고 부른다.
2.3 첫 번째 심층 신경망
2.3.1 데이터 적재
import numpy as np
from keras.utils import to_categorical
from keras.datasets import cifar10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
NUM_CLASSES = 10
x_train = x_train.astype('float32') / 255.0
x_test = t_test.astype('float32') / 255.0
y_train = to_categorical(y_train, NUM_CLASSES)
y_test = to_categorical(y_test, NUM_CLASSES)데이터의 마지막 차원은 컬러 채널이다. 이 데이터셋에는 행이나 열이 없다. 이런 배열을 4차원 텐서라고 부른다.
2.3.2 모델 생성
케라스 신경망 구조를 정의하는 두 가지 방법 Sequential, 함수형 API
Sequential : 일렬로 층을 쌓은 네트워크를 빠르게 만들 때 사용하기 좋다.
함수형 API : 여러 가지가 있는 네트워크의 생성, 층 설계의 완벽한 자유를 제공한다.
input_layer = Input((32,32,3))
x = Flatten()(input_layer)
x = Dense(200, activation = 'relu')(x)
x = Dense(150, activation = 'relu')(x)
output_layer = Dense(NUM_CLASSES, activation = 'softmax')(x)
model = Model(input_layer, output_layer)Input 층은 네트워크의 시작점, 네트워크가 기대하는 입력 데이터 크기를 튜플로 알려줘야 한다. 배치 크기는 지정하지 않는다. Input 층에 임의의 이미지 개수를 전달할 수 있기 때문에 배치 크기는 필요하지 않다.
Flatten 층은 입력을 하나의 벡터로 펼친다. 결과 벡터의 길이는 32*32*3이다. 이렇게 하는 이유는 Dense 층이 다차원 배열이 아닌 평평한 입력을 기대하기 때문이다.
Dense 층은 어떤 신경망에서든지 가장 기본적으로 사용되는 층이다. 이 층은 이전 층과 완전하게 연결되는 유닛을 가지고 있다. 그다음 비선형 활성화 함수를 통과하여 다음 층으로 전달된다. 이것이 없다면 선형 함수만 학습할 수 있을 것
활성화 함수는 대표적으로 렐루, 시그모이드, 소프트맥스가 존재한다.
렐루 rectified linear unit ReLU 활성화 함수는 입력이 음수이면 0이고 그 외는 입력을 출력한다.
시그모이드 sigmoid 활성화 함수는 출력을 0과 1사이로 조정하고 싶을 때 유용하다. 이진 분류나 다중 레이블 분류 문제에서 사용한다.
소프트맥스 활성화 함수는 층의 전체 출력 합이 1이 되어야 할 때 사용한다. 예를 들어샘플이 정확히 하나의 클래스에만 속해야 하는 다중 분류 문제이다. 이 함수는 다음과 같이 정의한다.

x = Dense(units=200)(x)
x = Activatoin('relu')(x)
or
x = Dense(units=200, activation='relu')(x)마지막 단계는 Model 클래스를 사용하여 모델 자체를 정의하는 것이다. 케라스에서 모델은 입력과 출력층으로 정의한다. 이 예제에서는입력 층으로 Input 층 하나를 정의했고 출력 층은 10개의 유닛을 가진 마지막 Dense 층이다.
Input 층의 크기는 x_train 의 크기와 맞아야 한다. 마지막 Dense 층의 출력 크기는 y_train 크기와 맞아야 한다. 이를 확인하기 위해 model.summary() 메서드를 사용해 각 층에 대한 정보를 확인할 수 있다.
Model: "model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 32, 32, 3)] 0
flatten (Flatten) (None, 3072) 0
dense (Dense) (None, 200) 614600
dense_1 (Dense) (None, 150) 30150
dense_2 (Dense) (None, 10) 1510
=================================================================
Total params: 646,260
Trainable params: 646,260
Non-trainable params: 0
_________________________________________________________________케라스는 None 을 사용하여 아직 네트워크에 전달된 샘플의 개수를 모른다는 것을 표시한다.실제로 샘플의 개수를 지정할 필요가 없다. 네트워크에 하나의 샘플을 전달하듯이 손쉽게 1,000 개를 전달할 수있다. 텐서 연산은 선형 대수를 사용해 동시에 모든 샘플에 수행되기 때문이다. GPU에서 훈련할 때 훈련 성능이 향상되는 이유이기도 하다.
summary 메서드를 통해 훈련될 파라미터의 수도 알려 준다.
2.3.3 모델 컴파일
이 단계에서는 모델에 손실 함수와 옵티마이저를 연결한다.
opt = Adam(lr=0.0005)
model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])손실 함수는 신경망이 예측 출력과 정답을 비교하는 데 사용된다. 케라스는 많은 손실 함수를 기본으로 제공하며 자신만의 손실 함수를 정의할 수도 있다. 가장 많이 사용하는 세 개의 손실 함수는 평균 제곱 오차, 범주형 크로스 엔트로피, 이진 크로스 엔트로피를 많이 사용한다.
회귀 문제의 경우 평균 제곱 오차 손실을 사용할 수 있다.


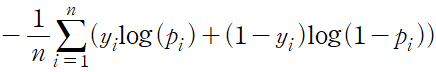
모델의 compile 메서드에 손실 함수와 옵티마이저를 전달한다. metrics 매개변수에는 정확도 같이 훈련 과정에 기록하고 싶은 지표를 추가로 지정할 수 있다.
2.3.4 모델 훈련
지금까지 네트워크의 구조를 정의하고 모델에 손실 함수와 옵티마이저를 연결했다.
모델을 훈련하기 위해 fit 메서드를 호출한다.
model.fit(x_train
, y_train
, batch_size=32
, epochs=10
, shuffle=True)2.3.5 모델 평가
새로운 데이터에 대한 성능 평가를 위해 evaluate 메서드를 사용한다.
model.evaluate(x_test, y_test)
>>>
313/313 [==============================] - 1s 3ms/step - loss: 1.4534 - accuracy: 0.4870
[1.4533861875534058, 0.4869999885559082]이 메서드의 출력은 모니터링한 측정값의 리스트이다. 여기서는 범주형 크로스 엔트로피 손실값과 정확도로 48%의 정확도를 달성했다.
predict 메서드를 사용해서 테스트 세트에 대한 예측 결과를 확인해볼 수 있다.
CLASSES = np.array(['airplane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck'])
preds = model.predict(x_test)
preds_single = CLASSES[np.argmax(preds, axis = -1)]
actual_single = CLASSES[np.argmax(y_test, axis = -1)]1. preds는 10000, 10 크기의 배열이다. 즉, 샘플마다 10개의 클래스 확률을 담은 벡터가 반환된다.
2. 이 확률 배열을 예측 결과로 바꾼다.
다음 코드를 통해 이미지와 예측값, 실제 레이블을 나란히 출력한다.
n_to_show = 10
indices = np.random.choice(range(len(x_test)), n_to_show)
fig = plt.figure(figsize=(15, 3))
fig.subplots_adjust(hspace=0.4, wspace=0.4)
for i, idx in enumerate(indices):
img = x_test[idx]
ax = fig.add_subplot(1, n_to_show, i+1)
ax.axis('off')
ax.text(0.5, -0.35, 'pred = ' + str(preds_single[idx]), fontsize=10, ha='center', transform=ax.transAxes)
ax.text(0.5, -0.7, 'act = ' + str(actual_single[idx]), fontsize=10, ha='center', transform=ax.transAxes)
ax.imshow(img)
2.4 모델 성능 향상
앞의 네트워크가 더 높은 성능을 내지 못하는 한 가지 이유는 입력 이미지의 공간 구조를 다룰 수 잇는 요소가 네트워크에 없기 때문이다. Dense 층에 전달하기 위해 첫 단계에서 이미지를 하나의 벡터로 펼쳤기 때문
이를 해결하기 위해 합성곱 층 convolution layer 를 사용해야 한다.
2.4.1 합성곱 층
합성곱은 필터의 이미지의 일부분과 픽셀끼리 곱한 후 결과를 더하는 것이다. 이미지 영역이 필터와 비슷할수록 큰 양수가 출력되고 필터와 반대일수록 큰 음수가 출력된다.
필터가 이동하면서 합성곱의 출력을 기록한다. 이를 통해 필터의 값에 따라 입력에서 어떤 특성을 골라낸 새로운 배열을 얻을 수 있다. 보통 하나의 필터보다 여러 개의 필터를 사용한다.
컬러 이미지를 사용하는 경우, 이미지에 있는 세 개의 채널에 맞춰 필터마다 세 개의 채널을 가진다. 케라스에서는 Conv2D 층을 사용해 높이와 너비를 가진 입력 텐서에 합성곱을 적용한다.
input_layer = Input(shape=(64, 64, 1))
conv_layer = Conv2D(
filters = 2,
kernel_size = (3,3),
strides = 1,
padding = 'same'
)(input_layer)스트라이드
필터가 한 번에 입력 위를 이동하는 크기, 크게할수록 출력 텐서의 크기가 줄어든다. 네트워크를 통과하면서 채널의 수는 늘리고 텐서의 공간 방햐야 크기를 줄이는 데 사용할 수 있다.
필터에 저장된 값은 훈련하는 동안 신경망이 학습하는 가중치이다. 랜덤하게 초기화되지만 점차 필터가 흥미로운 특성을 감지할 수 있도록 가중치를 조정해간다.
Conv2D 층의 출력도 (bath_size, height, width, filters) 크기의 4차원 텐서이므로 이 위에 Conv2D 층을 쌓아 신경망의 깊이를 더 키울 수 있다. 한 합성곱 층에서 다음 층으로 통과하면서 텐서의 크기가 어떻게 변하는지 이해하는 것이 중요하다.
input_layer = Input(shape=(32,32,3))
conv_layer_1 = Conv2D(
filters = 10
, kernel_size = (4,4)
, strides = 2
, padding = 'same'
)(input_layer)
conv_layer_2 = Conv2D(
filters = 20
, kernel_size = (3,3)
, strides = 2
, padding = 'same'
)(conv_layer_1)
flatten_layer = Flatten()(conv_layer_2)
output_layer = Dense(units=10, activation = 'softmax')(flatten_layer)
model = Model(input_layer, output_layer)
model.summary()
>>>
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) (None, 32, 32, 3) 0
_________________________________________________________________
conv2d_1 (Conv2D) (None, 16, 16, 10) 490
_________________________________________________________________
conv2d_2 (Conv2D) (None, 8, 8, 20) 1820
_________________________________________________________________
flatten_1 (Flatten) (None, 1280) 0
_________________________________________________________________
dense_1 (Dense) (None, 10) 12810
=================================================================
Total params: 15,120
Trainable params: 15,120
Non-trainable params: 0
_________________________________________________________________입력의 크기는 (None, 32, 32, 3)이다. 케라스는 None을 사용해 한꺼번에 임의의 개수의 이미지를 네트워크로 통과시킬 수 있다. 네트워크는 텐서에 대해 대수학 계산을 수행하기 때문에 이미지를 하나씩 전달할필요가 없다. 대신 여러 개를 묶어 배치로 전달한다.
첫 번째 합성곱 층의 필터 크기는 4*4*3 이다. 필터의 높이와 너비를 4로 선택했고, 이전 층의 채널이 3개이기 때문이다.(RGB) 이 층의 파라미터 수는 (4*4*3+1)*10 =490 개이다. 여기에서 +1은 필터마다 절편 항이 포함되기 때문이다. 필터의 깊이는 항상 이전 층의 채널 수와 같다.
입력 이미지의 4*4*3 영역에 적용된 각 필터의 출력은 필터의 가중치와 이미지에 덮인 영역의 픽셀끼리 곱한 값이 된다. strides = 2 이고 padding = same 이므로 출력의 높이와 너비는 16의 절반이 된다. 10개의 필터를 사용했으므로 배치 차원을 제외한 첫 번째 층의 출력 크기는 16, 16, 10 가 된다.
padding=same 인 합성곱 층의 출력 크기는 다음과 같이 계산한다.
(None, 입력 높이 / 스트라이드, 입력 너비 / 스트라이드, 필터개수)
두 번째 합성곱 층에선 필터 크기를 3*3 으로 선택했고 이전 층의 채널 수와 맞추기 위해 깊이는 10이 된다. 필터를 20개를 사용했기에 (3*3*10+1)*20 개의 파라미터를 가진다. 이 후 (None, 8, 8, 20) 가 된다.
일련의 Conv2D 층을 적용한 후 케라스의 Flatten 층을 사용해 텐서를 일렬로 펼쳐야 한다. 이를 통해 이를 통해 8*8*20=1280 유닛이 만들어지고 10개의 유닛과 소프트맥스 활성화 함수를 가진 Dense 층과 연결한다.
성능을 향상하기 위한 BatchNormalization 과 Dropout 층이 존재
2.4.2 배치 정규화 층
심층 신경망을 훈련할 때 대포적으로 어려운 한 가지는 네트워크의 가중치를 일정한 범위 안에서 유지해야 한다는 것이다. 값이 커지기 시작한다면 네트워크게 그레이디언트 폭주 현상이 발생한다.
이를 방지하기 위해 입력 스케일을 조정해 모든 층의 활성화 출력의 스케일을 안정시킬 수 있을 것이라 기대하지만, 네트워크가 훈련됨에 따라 가중치 값이 랜덤한 초깃값과 멀어지기 때문에 이러한 가정이 무너지기 시작한다. 이런 현상을 공변량 변화 covariate shift 라고 부른다.
안정을 유지하려면 네트워크가 가중치를 업데이트할 때 각 층은 암묵적으로 이전 층에서 온 입력의 분포가 훈련 반복에 상관없이 일정하다고 가정한다. 하지만 활성화 출력의 분포가 어떤 방향으로 심하게 이동할 수 있다.
배치 정규화 Batch normalization 은 이 문제를 해결한다. 배치 정규화 층은 배치에 대해 각 입력 채널별로 평균과 표준 편차를 계산한 다음 평균을 빼고 표준 편차로 나누어 정규화한다. 채널 별로 학습되는 두 개의 파라미터가 있다. 스케일 파라미터 gamma 와 이동 파라미터 beta 이다. 정규화한 입력을 gamma로 스케일을 조정하고 beta로 이동시켜 출력한다.
입력: 미니 배치에 포함된 x값: = {x_1...m};
학습 파라미터: r, b

BatchNormalization(momentum=0.9)momentum 매개변수는 평균과 표준 편차의 이동 평균을 계산할 때 이전 값에 주는 가중치다. 이동 평균을 v=*momentum+v_new*(1-momentum) 와 같이 계산된다. 이런 방식을 지수 이동 평균이라고 부른다. momentum이 클수록 이전 값의 비중이 크며 새로운 값에 대한 영향이 적다 기본값은 0.99이다.
2.4.3 드롭아웃 층
과대적합를 예방하기 위한 규제 기법 중 드롭아웃이 있다.
이전 층의 유닛 일부를 랜덤하게 선택하여 출력을 0으로 지정한다. 이는 네트워크가 특정 유닛 하나 혹은 일부에 과도하게 의존하지 않기 때문이다.
Dropout(rate=0.25)케라스에서의 구현, rate 매개변수는 이전 층에서 드롭아웃 할 유닛의 비율을 지정한다.
Dropout 층은 가중치 개수가 많아 과대적합되기 가장 쉬운 Dense 층 다음에 주로 사용된다.
2.4.4 합성곱, 배치 정규화, 드롭아웃 적용
input_layer = Input((32,32,3))
x = Conv2D(filters = 32, kernel_size = 3, strides = 1, padding = 'same')(input_layer)
x = BatchNormalization()(x)
x = LeakyReLU()(x)
x = Conv2D(filters = 32, kernel_size = 3, strides = 2, padding = 'same')(x)
x = BatchNormalization()(x)
x = LeakyReLU()(x)
x = Conv2D(filters = 64, kernel_size = 3, strides = 1, padding = 'same')(x)
x = BatchNormalization()(x)
x = LeakyReLU()(x)
x = Conv2D(filters = 64, kernel_size = 3, strides = 2, padding = 'same')(x)
x = BatchNormalization()(x)
x = LeakyReLU()(x)
x = Flatten()(x)
x = Dense(128)(x)
x = BatchNormalization()(x)
x = LeakyReLU()(x)
x = Dropout(rate = 0.5)(x)
x = Dense(NUM_CLASSES)(x)
output_layer = Activation('softmax')(x)
model = Model(input_layer, output_layer)
model.summary()
>>>
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_2 (InputLayer) (None, 32, 32, 3) 0
_________________________________________________________________
conv2d_3 (Conv2D) (None, 32, 32, 32) 896
_________________________________________________________________
batch_normalization_1 (Batch (None, 32, 32, 32) 128
_________________________________________________________________
leaky_re_lu_1 (LeakyReLU) (None, 32, 32, 32) 0
_________________________________________________________________
conv2d_4 (Conv2D) (None, 16, 16, 32) 9248
_________________________________________________________________
batch_normalization_2 (Batch (None, 16, 16, 32) 128
_________________________________________________________________
leaky_re_lu_2 (LeakyReLU) (None, 16, 16, 32) 0
_________________________________________________________________
conv2d_5 (Conv2D) (None, 16, 16, 64) 18496
_________________________________________________________________
batch_normalization_3 (Batch (None, 16, 16, 64) 256
_________________________________________________________________
leaky_re_lu_3 (LeakyReLU) (None, 16, 16, 64) 0
_________________________________________________________________
conv2d_6 (Conv2D) (None, 8, 8, 64) 36928
_________________________________________________________________
batch_normalization_4 (Batch (None, 8, 8, 64) 256
_________________________________________________________________
leaky_re_lu_4 (LeakyReLU) (None, 8, 8, 64) 0
_________________________________________________________________
flatten_2 (Flatten) (None, 4096) 0
_________________________________________________________________
dense_2 (Dense) (None, 128) 524416
_________________________________________________________________
batch_normalization_5 (Batch (None, 128) 512
_________________________________________________________________
leaky_re_lu_5 (LeakyReLU) (None, 128) 0
_________________________________________________________________
dropout_1 (Dropout) (None, 128) 0
_________________________________________________________________
dense_3 (Dense) (None, 10) 1290
_________________________________________________________________
activation_1 (Activation) (None, 10) 0
=================================================================
Total params: 592,554
Trainable params: 591,914
Non-trainable params: 640
_________________________________________________________________더 높은 정확도를 달성한 것을 확인할 수 있다. 간단하게 합성곱, 배치 정규화, 드롭아웃 층을 모델 구조에 추가하여 성능을 향상, 이전 모델보다 층은 늘었지만 파라미터의 개수는 더 줄었다.(훈련 시간을 비교해볼 수 있을 듯)