최대 가능도와 최소 제곱

제곱합 오류 함수를 최소화하는 방식으로 데이터 집합에 다항 함수를 근사한다.

가우시안 노이즈 모델을 가정했을 경우 이 오류 함수를 최소화하는 것이 최대 가능도 해를 구하는 것에 해당하는 것도 증명되었다. 해당 논의로 돌아가서 최소 제곱법과 최대 가능도 방법의 관계에 대해 자세히 살펴본다.

타깃 변수 t 는 결정 함수 y(x,w) 와 가우시안 노이즈의 합으로 주어진다고 가정한다.

epsilon 은 0을 평균으로, beta 를 정밀도 (분산의 역) 으로 가지는 가우시안 확률 변수다. 

따라서 다음과 같이 적을 수 있다.

제곱 오류 함수를 가정할 경우 새 변수 x 에 대한 최적의 예측값은 타깃 변수의 조건부 평균으로 주어질 것이다. 

위 식의 형태의 가우시안 조건부 분포의 경우 조건부 평균은 다음과 같다.

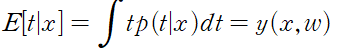
노이즈의 분포가 가우시안이라는 가정은 x 가 주어졌을 때의 t 의 조건부 분포가 단봉 형태임을 내포하고 있다. 

입력 데이터 집합 X 과 그에 해당하는 타깃 변수 t 를 고려해본다. 타깃 변수들은 열벡터로 무리지을 수 있다. 

이 가능도 함수는 조절 가능한 매개변수 w 와 beta 의 ㅎ마수다.

회귀나 분류 같은 지도 학습 문제의 경우에 우리는 입력 변수의 분포를 모델하려 하지 않는다. 따라서 x 는 언제나 조건부 변수의 집합에 포함되어 있을 것이다. 

그러므로 표현식에서 x 를 뺄 수 있다. 

가능도 함수에 대해 로그를 취하고 단변량 가우시안의 표준 형태 식을 이용하면 다음을 얻을 수 있다.

여기서 제곱합 오류 함수는 다음과 같이 정의된다. 

 

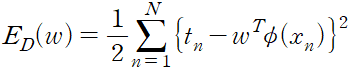
이제 여기에 최대 가능도 방법을 적용하여 w 와 beta 를 구할 수 있다.

첫 번째로 w 에 대해 극대화하는 경우를 고려해본다. 

가우시안 노이즈 분포하에서 선형 모델에 대해 가능도 함수를 최대화하는 것은 제곱합 오류 함수를 최소화하는 것과 동일하다. 

로그 가능도 함수의 기울기는 다음과 같다.

기울기를 0 으로 놓으면 다음을 얻게 된다.

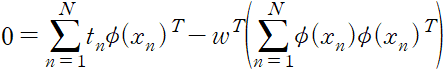
이를 w 에 대해 풀면 다음을 얻을 수 있다.

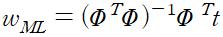
위 식을 최소 제곱 문제의 정규 방정식이라고 부른다. 여기서 PHI 는 N*M 행렬로 설계 행렬 이라고 불린다.

설계 행렬의 각 원소는 PHI_nj = phi_j(x_n) 으로 주어진다.

위 식을 행렬 PHI 의 무어-펜로즈 유사-역 이라고 한다. 

역행렬의 개념을 정사각이 아닌 행렬들에 대해서 일반화 한 것이라고 보면 된다.

 

편향 매개변수 w_0 의 역할에 대해 살펴본다. 편향 매개변수를 명시화하면 오류 함수를 다음과 같이 적을 수 있다.

w_0 에 대한 미분값을 0으로 놓고 w_0 에 대해 풀면 다음을 구할 수 있다.

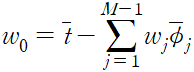
여기서 다음을 정의

편향이 훈련 집합의 타깃 변수들의 평균과 기저 함숫값 평균들의 가중 합 사이의 차이를 보상한다는 것을 알 수 있다.

 

로그 가능도 함수를 노이즈 정밀도 매개변수 beta 에 대해 최대화하면 다음을 얻게 된다.

노이즈 정밀도의 역이 회귀 함수 근처 타깃 변수들의 잔차 분산으로 주어진다는 것을 알 수 있다.