이산 확률 변수(discrete random variable)
하나의 이진 확률 변수 x ∈ {0,1} 을 고려해 본다. x 는 동전 던지기의 결괏값을 설명하는 확률 변수일 수 있다.
만약 동전의 앞 뒷면의 나올 확률이 동일하지 않다고 가정, 이때, x = 1 일 확률은 매개변수 u 를 통해 다음과 같이 표현할 수 있다.

x 에 대한 확률 분포를 다음의 형태로 적을 수 있다.
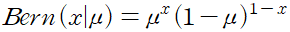
이것을 베르누이 분포 Bernoulli distribution 라고 한다.
mu = 0.7
Bern_x = mu**1 * (1-mu)**(1-1)
Bern_x
>>>
0.7
MU = np.array(([0.7],[0.3]))
MU
>>>
array([[0.7],
[0.3]])
X = np.array(([0],[1]))
X
>>>
array([[0],
[1]])
Bern = MU**X * (1-MU)**(1-X)
Bern
>>>
array([[0.3],
[0.3]])
MU**X
>>>
array([[1. ],
[0.3]])
1 - MU
>>>
array([[0.3],
[0.7]])
1 - X
>>>
array([[1],
[0]])
(1 - MU)**(1-X)
>>>
array([[0.3],
[1. ]])베르누이 분포는 정규화되어 있으며, 그 평균과 분산이 다음과 같이 주어진다는 것을 볼 수 있다.
E[x] = mu,
var[x] = mu(1-mu)
x 의 관측값 데이터 집합 D = {x_1, ...,x_n} 이 주어졌다고 하자. 관측값들이 p(x|mu) 에서 독립적으로 추출되었다는 가정하에 mu 의 함수로써 가능도 함수를 구성할 수 있다.

빈도적 관점에서는 가능도 함수를 최대화하는 mu 를 찾아서 mu 의 값을 추정할 수 있다.
베르누이 분포의 경우 로그 가능도 함수는 다음으로 주어진다.

로그 가능도 함수는 오직 관측값들의 합인 x_n 을 통해서만 N 개의 관측값 x_n 과 연관된다는 점에 주목할 필요가 있다.
이 합은 충분 통계량 sufficient statistic 의 예시 중 하나다.
ln p(D|mu) 를 mu 에 대해 미분하고 이를 0 과 같다고 놓으면 다음과 같은 최대 가능도 추정값을 구할 수 있다.
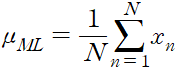
위 식은 표본 평균이라고도 불린다. 데이터에서 x = 1 인 관찰값의 수를 m 이라고 하면 식을 다음의 형태로 다시 적을 수 있다.

즉, 최대 가능도 체계하에서 동전의 앞면이 나올 확률은 데이터 집합에서 앞면이 나온 비율로 주어지게 되는 것이다.
data = np.concatenate((ones, zeros), axis=1)
data
>>>
array([[1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0.]])
a,b = np.where(data==0)
a
>>>
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0])
c, d = np.where(data == 1)
c
>>>
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0])mu_ML = np.array(([c.shape[0] / data.shape[1]], [a.shape[0] / data.shape[1]]))
mu_ML
>>>
array([[0.7],
[0.3]])
크기 N 의 데이터가 주어졌을 때 x = 1 인 관측값의 수 m 에 대해서도 분포를 생각해볼 수 있다. 이를 이항 분포 binomial distribution 라 한다.
정규화 계수를 구하기 위해서는 동전 던지기를 N 번 했을 대 앞면이 m 번 나올 수 있는 가능한 모든 가짓수를 구해야 한다. 따라서 이항 분포를 다음과 같이 적을 수 있다.


위 식은 N 개의 물체들 중에서 m 개의 물체를 선별하는 가짓수를 구한 것이다.