7. 황금 열쇠와 개선된 소수 정리
1. 에라토스테네스의 체, 황금 열쇠란 에라토스테네스의 체를 해석학의 언어로 표현하는 방법을 칭하는 말로서, 이 방법은 레온하르트 오일러에 의해 발견되었다.
에라토스테네스의 체~~~
위 과정을 계속 진행, 숫자를 일일히 헤아리지 않고 리만 제타 함수를 이용한다. 1보다 큰 임의의 함수 s 에 대한 제타 함수는 다음과 같다.

제타 함수에는 모든 양의 정수들이 각 항의 분모에 자리 잡고 있다.
양변에 1/2^s 를 곱해본다.

이 다음 첫 번째 식에서 두 번째 식을 빼본다.

위와 같은 형태가 된다. 에라토스테네스의 체를 이용, 1/3^s 를 곱하고, 빼고의 반복...
매 단계마다 뺄셈이란 연산을 거친다. 큰 소수까지 반복, 이 과정을 무한히 반복하면 1의 결과를 얻을 수 있다고 짐작할 수 있다.

s 는 1보다 큰 임의의 수이고, 좌변에 곱해진 괄호들은 모든 소수에 하나씩 대응되면서 무한히 계속된다. 좌변에 나타나 있는 모든 괄호들로 양변을 나누면 제타함수가 다음과 같은 형태로 얻어진다.

이것이 황금 열쇠의 정체이다.
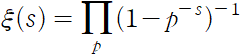

좌변의 합과 우변의 곱은 모두 무한히 행해진다. 이것은 소수의 개수가 무한히 많다는 것을 증명하는 결과이기도 하다.
만일 소수의 명단이 끝난다면 우변의 곱도 끝날 것이고, 따라서 s 가 어떤 값이건 간에 우변은 유한한 개수의 수들이 곱해진 형태를 띠게 될 것이다. 그러나 s = 1 일 때 좌변은 조화급수가 되어 무한으로 발산한다. 그렇다면 우변도 무한이 되어야 하는데, 유한한 개수의 수를 곱하여 무한의 결과가 나오지 않기에 ㅐ소수의 개수는 무한하다는 결론을 내릴 수 있다.
좌변은 모든 양의 정수에 대한 합인 반면, 우변은 모든 소수에 대한 곱의 형태로 되어있다.
위 식의 원래 이름은 오일러의 곱셈 공식이다.
미분의 이해,
곡선의 기울기 gradient 는 각 지점마다 다르다. 그러나 한 지점에서의 기울기를 따진다면 어느 지점에서나 하나의 명확한 값을 가진다.
직선의 기울기는 수직 방향으로 상승한 높이를 수평 방향의 이동 거리로 나눈 값으로 정의한다.
곡선 위의 한 지점에서 기울기를 구하기 위해 그 지점에서 곡선에 접하는 직선을 그린다. (접선) 각 위치에서 직선의 기울기가 그 지점에서의 곡선의 기울기에 해당한다.
미적분학의 출발점은 다음과 같다.
임의의 함수 f 가 주어졌을 때, 약간의 변형을 가하면 모든 지점에서 f 의 기울기를 나타내는 g 라는 함수를 구할 수 있다. 함수 g 를 f 의 도함수 derivative 라고 한다. 도함수 g 를 구하는 과정을 미분 differentiation 라고 한다.
함수 f 를 미분하여 g 라는 함수가 얻어졌다고 해 본다. 그러면 g 는 f 의 도함수가 된다. 이는 적분 함수 integral 이다. 도함수의 역은 적분 함수이며, 미분의 역은 적분이라고 한다.
함수 f 의 도함수 g 는 임의의 지점에서 f 의 기울기를 말해준다. 적분은 그래프 아랫부분의 넓이를 구할 때 사용할 수 있다.