4.3 기울기 벡터 기반 최적화
대부분의 심층 학습 알고리즘에는 어떤 형태로는 최저고하가 관여한다. 최적화는 x 의 값을 바꾸어 가면서 어떤 함수 f(x) 의 값을 최대화 또는 최소화하는 것을 말한다. 그런데 일반적으로 대부분의 최적화 문제는 f(x) 를 최소화하는 것을 기준ㅇ로 설명한다. 최대화의 경우 반대
최소화 또는 최대화할 함수를 목적함수 또는 판정기준 이라고 부른다. 최소화의 경우 그러한 함수를 ㅣㅂ용함수나 손실함수, 오차함수라고 부르기도 한다.
함수를 최소화 또는 최대화하는 인수의 값에 흔히 위 첨자 *를 붙인다. 예를 들어 x*=argmin f(x) 이다.
y = f(x) 라는 함수가 있다고 하자. 여기서 x 와 y 는 둘 다 실수, 이 함수의 미분을 f'(x) 또는 dy/dx 로 표기한다. 미분 f'(x) 는 점 x 에서의 f(x) 기울기를 뜻한다.
미분은 입력의 변화에 비례해서 출력이 얼마나 변하는지를 말해준다.
이러한 미분 함수는 최소화에 유용, 도함수는 출력 y 를 좀 더 개선하려면 x 를 얼마나 변화해야 하는지 말해 주기 때문, x 를 미분과는 부호가 반대인 방향으로 작은 단계만큼 이동함으로 f(x) 의 값을 줄일 수 있다. 이런 기법을 경사 하강법이라고 부른다.
f'(x) 인 점을 임계점, 정류점이라고 부른다 그리고 f(x) 가 모든 이웃 점보다 작은 점을 local minimum point 라고 부른다.
입력이 여러 개인 함수를 최적화할 때도 많다. 최소화의 개념이 성립하려면 그러한 함수의 출력은 반드시 하나의 값이어야 한다.
함수의 입력이 여러 개일 때는 편미분의 개념을 사용해야 한다.
미분의 개념을 입력이 여러 개인 함수로 일반화한 것을 기울기 벡터라고 부른다. f 의 기울기는 모든 편미분으로 구서된 벡터, 기울기 벡터의 각 성분은 f 의 편미분이다. 다차원 입력 함수에서 임계점은 기울기 벡터의 모든 성분이 0인 점이다.
함수 f 의 u 방향 기울기를 u 방향의 방향미분이라고 부른다.
다른 말로 하면, 방향미분을 a 에 대한 f(x+au) 의 도함수를 a= 0 에서 평가한 것이다.
f 를 최소화하려면 f 가 가장 빠르게 감소하는 방향을 찾아야 한다. 방향 미분을 사용하면 그러한 방향을 알 수 있다.

이 공식에 ||u||_2 = 1 을 대입하고 u 에 의존하지 않는 인수들을 생략해서 정의하면 min_u cos theta 가 나온다. 이 값은 u 가 기울기의 반대 방향 때 최소가 된다.
최대 경사법은 기울기 벡터의 모든 성분이 0이면 수렴한다. 때에 따라서는 이러한 반복 알고리즘을 실행하는 대신 방정식을 x 에 대해 풀어서 임계점으로 직접 이동할 수도 있다.
경사 하강법은 연속 공간 함수의 최적화에만 적용할 수 있지만, 작은 단계의 이동을 반복해서 더 나은 인수 조합을 찾는다는 일반적인 개념은 이산 공간에도 적용할 수 있다.
4.3.1 야코비 행렬과 헤세 행렬
입력 뿐만 아니라 출력도 벡터인 함수의 편미분들을 모두 구해야 할 때가 있다. 그런 모든 편미분으로 구성된 행렬ㅇ르 야코비 행렬이라고 부른다.
구체적으로 f:R^m → R^n 의 야코비 행렬 J 는 J_i,j = partial / (partial x_j) * f(x)_i 로 정의된다.
미분의 미분이 유용할 때도 있다. 그런 도함수를 이차미분이라고 부른다. 이러하나 이차미분은 일차미분이 입력의 변화에 따라 어떻게 변하는지를 말해준다. 그러한 정보는 경사 하강법의 한 단계가 우리가 기울기에만 근거해서 기대한 만큼이나 해를 개선할 것인지 알려준다는 점에서 중요하다.
이차미분을 곡률의 측도로 간주할 수 있다.
함수의 입력이 다차원이며 이차미분이 여러 개이다. 그러한 이차미분들을 하나의 행렬로 모은 것을 헤세 행렬이라고 부른다.
다른 말로 하면 헤세 행렬은 기울기의 야코비 행렬이다.
헤세 행렬 H(f)(x) 는 다음과 같이 정의된다.

이차편미분이 연속인 모든 점에서는 미분 연산자가 가환적이다. 즉, 미분 연산자가 교환법칙을 만족하므로 순서를 바꾸어도 된다.
이는 H_i,j = H_j,i 라는 뜻으로 그런 점들에서는 헤세 행렬에 대칭행렬이다.
심층 학습 맥락에서 만난느 대부분의 함수는 거의 모든 점에서 헤세 행렬이 대칭행렬이다.
그리고 헤세 행렬이 실숫값 대칭해열ㄹ일 때는 헤세 행렬을 실수 고윳값들의 집합과 고유벡터들로 이뤄진 직교 기저로 분해할 수 있다.
단위벡터 d 가 가리니큰 특정 방향의 이차미분 d^T HD 로 표기한다. d 가 H 의 한 고유벡터일 때, 그 방향의 이차미분은 그 고유벡터에 해당하는 고윳값이다. d 가 그 외의 방향일 때는 방향 이차미분이 모든 고윳값의 가중평균인데, 이때 가중치들은 0에서 1 사이의 값이고 고유벡터와 d 사이의 각도가 작을수록 해당 가중치가 크다.
최대 고윳값은 최대 이차미분을 결정하며, 최소 고윳값은 최소 이차미분을 결정한다.
방향이 있는 이차미분은 하나의 경사 하강 단계로 어느 정도의 효과를 볼 수 있을지를 말해 준다. 현재 점 x^(0) 주변의 함수 f(x) 를 다음처럼 이차 테일러 급수로 근사할 수 있다.

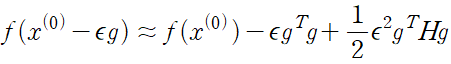
이 공식에는 세 개의 항
하나는 함수의 원래 값이고
다른 하나는 함수의 기울기에 따라 예측한 개선 정도,
나머지 하나는 함수의 곡률에 의한 오차를 바로잡기 위한 값이다. 이 보정 값이 너무 크면, 경사 하강에 의해 오히려 언덕 위로 이동하 ㄹ여지가 있다.
gHg 가 0이나 음수일 때, 이 테일러 급수 근사는 e 를 영원히 증가하면 f 가 영원히 감소함을 뜻한다. 실제 응용에서는 e 가 크면 테일러 급수의 정확성이 떨어질 가능성이 크다.
그런 경우 발견법적인 방법을 사용해서 좀 더 나은 e 값을 선택할 필요가 있다.
gHg 가 양수일 때, 함수의 테일러 급수 근사를 가장 많이 감소하는 최적의 단계 크기는 다음과 같다.

최악의 경우, 즉 g 가 최대 고윳값에 대응되는 H 의 고유벡터와 같은 방향인 경우, 이 최적 단계 크기는 1 / lambda 이다.
따라서 최소화할 함수를 이차함수로 잘 근사할 수 있는 한, 헤세 행렬의 고윳값들은 학습 속도의 규모를 결정한다.
주어진 이계점의 종류를 결정할 때 이차미분을 사용할 수도 있다. 이차미분이 양수일 때 일차도함수는 오른쪽으로 이동하면 증가, 왼쪽으로 이동시 감소
즉, 충분히 작은 e 에 대해 f'(x-e) < 0 이다.
그러므로 f'(x) = 0, f''(x) > 0 일 때는 x 가 극소점이라고 결론지을 수 있다. 이런 판정을 이차미분 판정이라고 부른다.
입력이 다차원일 경우 함수의 모든 이차미분을 조사해야 한다. 헤세 행렬의 고윳값 분해를 이용하면 이차미분 판정을 다차원의 경우로 일반화할 수 있다.
구체적으로 말하면, ㅁf(x) = 0 이 되느 임계점에서 헤세 행렬의 고윳값들을 보면 그 임계점의 종류를 알 수 있다.
헤세 행렬이 양의 정부호 행렬이면 그 점은 극소점이다. 극소점에서는 임의의 방향의 이차방향미분이 반드시 양수이어야 한다는 사실과 단변량 이차미분 판정의 원리를 생각하면 이를 이해할 수 있다.
다차원에서는 주어진 임계점이 안장점임을 말해주는 증걸르 찾는 것이 가능할 때도 있다. 적어도 하나의 고윳값이 양수이고 적어도 하나의 고윳값이 음수이면, x 가 f 의 어떤 한 단면에서는 그대점이고 다른 어떤 한 단면에서는 극소점일 것임이 틀림없다.
다차원에서는 한 점의 여러 방향마다 각자 다른 이차미분이 있다. 그 점에서의 헤세 행렬의 조건수는 그 이차미분들이 서로 얼마나 다른지 나타내는 측도이다. 헤세 행렬의 조건수가 나쁘면 경사 하강법의 성과도 나쁘다. 그런 경우 한 방향에서는 미분이 빠르게 증가하지만 다른 방향에서는 느리게 증가하기 때문,
경사 하강법은 미분들의 그러한 변화를 알아채지 못하므로, 미분이 더 오랫동안 음수를 유지하는 방향으ㅡ로 이동하는 것이 바람직하다는 점도 알아채지 못한다.
조건수가 나쁘면 좋은 단계 크기를 선택하기도 어렵다. 단계 크기는 극소점을 지나치지 않을 정도로, 그리고 큰 양의 곡률 때문에 언덕 위로 올라가는 일이 없을 정도로 작아야 한다.
이 문제는 헤세 행렬에 있는 정볼르 이용해서 검색 방향을 결정함으로써 해결할 수 있다. 그런 접근 방식 중 가장 간단한 방법이 뉴턴법이다.
뉴턴법은 이차 테일러 급수 전개를 이용해서 어떤 점 근처의 f(x) 를 근사한다.
경사 하강ㅂ버처럼 기울기만 사용하는 최적화 알고리즘들을 통칭해서 일차 최적화 알고리즘이라고 부른다. 뉴턴법처럼 헤세 행렬도 사용하는 최적화 알고리즘을 이차 최적화 알고리즘이라고 부른다.
최적화 알고리즘들은 다양한 함수들에 적용할 수 있지만, 제공하는 보장은 거의 없다. 대체로 심층 학습 알고리즘들은 보장이 없는 경우가 많은데 이는 심층 학습에 쓰이는 함수들이 상당히 복잡한 함수의 부류에 속하기 때문이다.
반면, 다른 여러 분야에서는 제한된 부류의 함수들에만 적용할 수 있도록 최적화 알고리즘을 설계하는 것이 주된 최적화 접근 방식이다.
볼록 함수 최적화 알고리즘은 좀 더 강한 제약을 둠으로써 더 많은 보장을 제공한다. 이 알고리즘들은 볼록함수, 헤세 행렬이 모든 점에서 양의 준정부호인 함수에만 적용된다. 그러나 심층 학습의 대부분의 문제들은 볼록함수 최적화의 형태로 표현하기 어렵다.