정규 방정식 normal equation

선형 회귀 모델에서 각 피처의 가중치와 편향을 구해야 한다. 이는 가중치 w 벡터로 표현

가중치는 트레이닝 데이터로부터 최소 제곱법을 사용해 구할 수 있다. 최소 제곱법은 오차의 제곱합이 최소가 되는 추정량을 구하는 방법,

먼저 전체 식에서 오차를 구하면 아래와 같다.

실제 타깃 데이터값 y는 학습을 통해 구한 모형에 오차를 더한 값

오차 제곱합의 표현

 

최소 제곱법을 사용해 구한 가중치를 최소 제곱 추정량 least squareds estimator 이라고 하고 이를 행렬로 확장하면 다음과 같다.

행렬 X는 데이터 x와 b를 합친 형태, 가중치 벡터도 기존 가중치와 b를 합친 형태 

행렬 X는 (n, (p+1)) 차원이며, 타깃 벡터 y는 (n, 1) 차원, 가중치 벡터는 (p+1, 1) 차원이다. 

이를 다시 수식으로 표현, y = Xw

이 수식을 최적화해 구한 가중치의 추정량은 아래와 같다 argmin

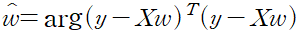
실제 값과 예측 값의 차이의 제곱, 오차 제곱 합이 최소가되는 함수

 

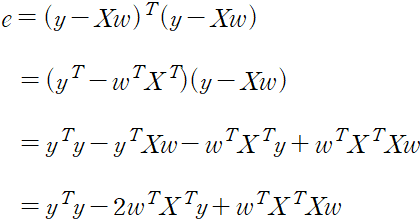
서로가 서로를 전치한 행렬이므로 스칼라 값이 동일, 합칠 수 있다.

최적의 가중치를 귀하려면 위 식의 미분 값이 0이 되어야 한다.

 

위 식이 0이 되기 위한 값

 

파이썬 구현

X = 2 * np.random.rand(100,1)
y = 4 + 3 * X + np.random.randn(100,1)

X_b = np.c_[np.ones((100, 1)), X]
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
theta_best
>>>
array([[4.27935698],
       [2.91138471]])