최적화(미완)

개념 정리

최적화(미완)

명징직조지훈 2022. 10. 26. 23:07

1.컨벡스 셋

1.1 직선과 선분

머신러닝의 궁극적인 목표는 최적화 optimization

처음으로 배울 개념은 컨벡스 셋으로 먼저 직선과 선분에 대해 다룬다. 직선은 시작과 끝 지점이 존재하지 않는 반면, 선분은 시작과 끝 지점이 존재하는 것을 의미한다.

직선과 선분은 컨벡스를 설명할 때 중요한 역할을 한다. 공간 R^n 에서 두 점 x1,x2를 잇는 선 사이에 있는 점을 아래와 같이 표현

만약 w=0 이면 y=x2가 되고 w=1이면 y=x1 이 된다. 만약 0<=w<=1 이면, x1, x2 간의 선분이 된다. 그리고 w∈R 이라면 즉, w 값의 범위 제한이 없으면 직선이 된다.

두 점을 잇는 굵은 선은 선분을 나타낸다. w는 가중치라고 생각할 수 있다. 선분과 외부 점을 모두 연결한 선 전체를 직선이라고 한다. 직선에는 w 값의 제한이 없으므로 0보다 작은 음수 값을 가질 수 있고 1보다 큰 값을 가질 수 있다.

1.2 아핀 셋

2차원 공간을 생각, 집합 C 내부의 두 점을 잇는 직선이 있다고 햇을 때, wx1+(1-w)x2∈C 이면 집합 C는 아핀 셋이다. 이는 두 점 x1, x2 를 잇는 직선은 집합 C에 포함되어야 한다는 뜻이다. w 값의 제한이 없으므로 선분이 아닌 직선에 해당한다.

회색 영역은 아핀 셋을 나타낸다. 아핀 셋은 시작과 끝 범위 제한이 없는 직선을 포함하므로 아핀 셋 역시 범위 제한이 없다. n 차원으로 확장하면 w1x1+...+wnxn 으로 쓸 수 있고, 이때 w1+...+wn=1 을 만족한다. 이를 포인트 x1...xn 에 대한 아핀 조합 affine combination 라고 한다.

즉 아핀 셋은 내부에 존재하는 점들에 대한 모든 아핀 조합을 포함한다.

아핀 조합은 곧 집합 C에 속하는 점들의 선형 결합과 같다. 그리고 선형 결합 계수 w들의 합은 1을 만족한다.

예를 들어 집합 C가 아핀 셋이라고 했을 때 포인트 x1,...,xn이 집합 C에 속하고 sum(wn)=1 을 만족할 때, 아핀 조합 또한 집합 C에 속한다.

1.3 아핀 함수 vs 선형 함수

아핀 함수와 선형 함수의 차이

함수 f:R^n→R^m 이 존재한다고 할 때 함수 f는 n차원에서 m차원으로 변환하는 함수이다.

위와 같은 함수가 존재할 때, 함수 f의 정의역 domain 을 dom f 라고 한다. 위 함수 f의 의미는 n차원 공간 R^n 에 속하는 벡터를 m 차원 공간 R^m 에 속하는 벡터로 변환한다는 뜻이다.

함수 f가 선형 변환이라면 n*m 행렬로 나타낼 수 있으며 이 행렬을 W라고 표현한다.

데이터 포인트 x를 선형 변환하는 선형 함수는 위와 같은 식으로 나타낼 수 있다.

한편, 아핀 함수가 선형 함수와 다른 점은 상수항 b가 추가되는 것

데이터 포인트 x를 아핀 변환하는 아핀 함수를 식으로 나타내면 그림으로 나타내면

선형 변환의 경우 원점을 지난다. 아핀공간의 경우 상수b 에 의해 y 절편이 존재한다.

1.4 컨벡스 셋

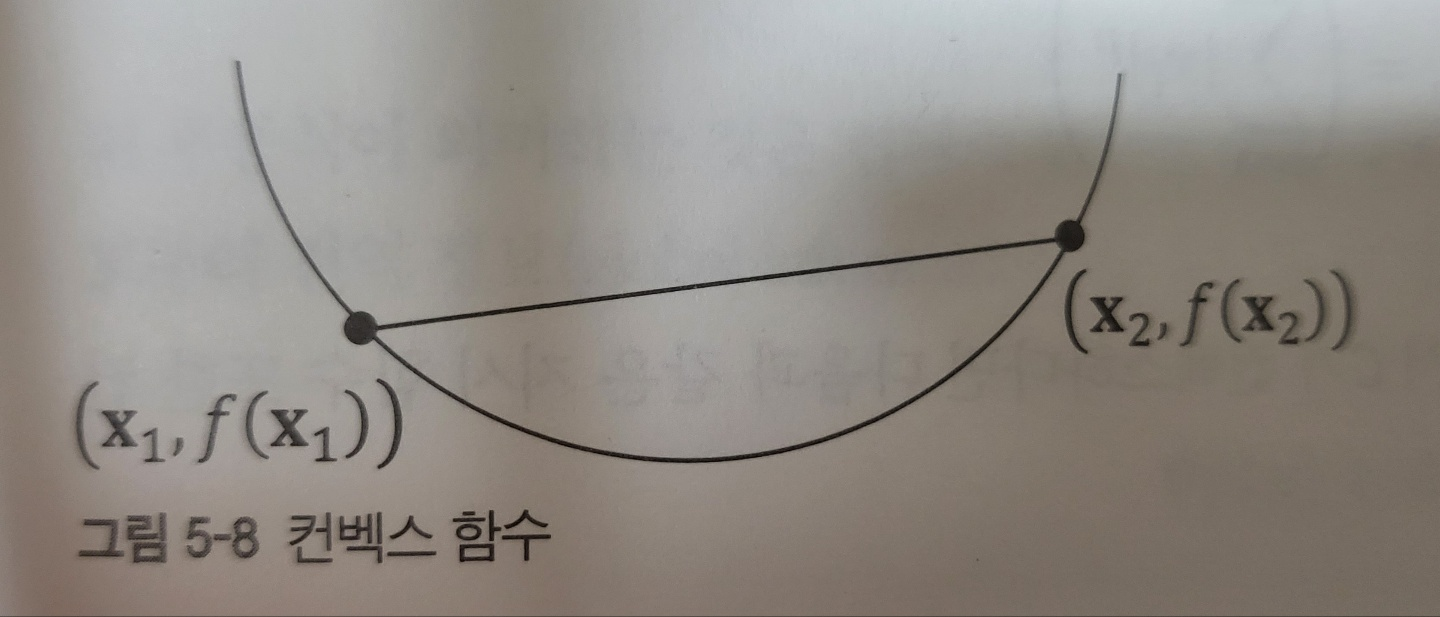
만약 집합 C 내부의 두 점 사이의 선분이 집합 C에 속한다면 집합 C는 컨벡스하다.

즉, 두 점 x1,x2∈C 에 대해 0<=w<= 1을 만족하는 w에 대해 아래 조건을 만족하면 C를 컨벡스 셋이라고 한다.

두 점을 잇는 직선을 포함하는 아핀 셋과는 달리 컨벡스 셋은 두 점 사이의 선분을 포함한다는 것이다.

컨벡스 셋의 정의에서 가중치 w 값의 범위 제한이 있다. 즉, 컨벡스 셋 내의 모든 두 점을 이었을 때, 해당 선분이 집합 내에 속해야 한다는 뜻이다.

아핀 조합과 비슷한 개념으로 컨벡스 조합이라는 개념도 존재한다.

1.5 초평면과 반공간

초평면은 서포트 벡터 머신 알고리즘에 핵심적인 개념이다. 초평면은 아래와 같은 집합을 말한다.

초평면이란 위 식을 만족하는 데이터 포인트 x의 집합을 의미한다. 이때, w는 n 차원 가중치 벡터이고 b 는 1차원 스칼라값이다. 이때, w^Tx=b 는 벡터 w와 벡터 x를 내적한 값이 b라는 것을 의미한다.

여기서 내적값이 b가 아니라 0이라면 계산이 편리할 것, 초평면의 형태를 아래와 같이 바꿀 수 있다.

x0는 초평면 내의 어떤 점도 가능하다.

내적값이 0이면 두 벡터는 수직이다. 위 그림을 보면 벡터 w는 벡터 x-x0 과 수직이므로 두 벡터를 내적했을 때 0이라는 것을 알 수 있다.

전체 공간은 초평면에 의해 두 개의 반공간으로 나뉜다. 초평면이 두 공간을 나누는 경계라고 생각하면, 반공간은 초평면으로 나뉜 공간의 일부분을 나타낸다고 볼 수 있다.

즉, 반공간은 아래와 같은 형태로 표현한다.

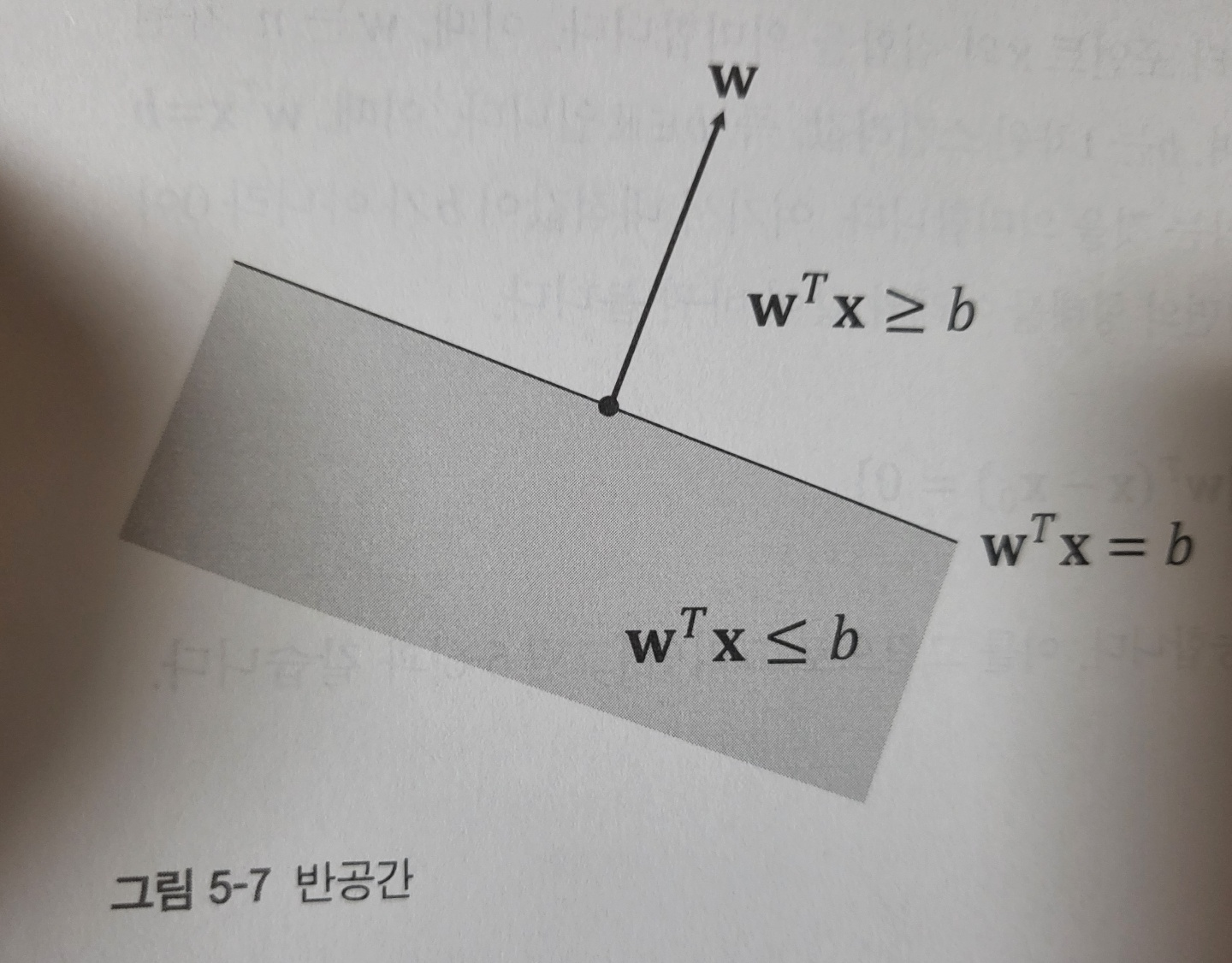
위 그림은 반공간을 나타낸다. 초평면에 의해 나뉜 반공간은 컨벡스 셋이지만 아핀 셋은 아니다. 왜냐하면 아핀 셋이 되려면 공간의 제한이 없어야 하는데, 반공간에는 경계가 존재하기 때문

초평면과 반공간은 서로 연관되어 있으며 분류, 회귀 문제를 풀 때 핵심적인 개념이다.

여러 머신러닝의 목적은 전체 공간을 효과적으로 나눌 수 있는 초평면을 찾는 문제

2. 컨벡스 함수

2.1 컨벡스 함수의 개념

함수 f의 정의역이 컨벡스 셋(convex set)이고, 모든 데이터 포인트 x1,x2, 0<=w<=1 에 대해

를 만족하는 함수 f:R^n→R 을 컨벡스하다고 말한다. 위 부등식의 의미는 두 점(x2,f(x2)),(x2,f(x2)) 사이의 선분이 함수 f의 그래프보다 위에 있어야 한다는 뜻이다.

위 부등호에서 아래 식과 같이 등호가 없고 0<=w<=1 이면 strictly 컨벡스하다고 말한다.

반대되는 개념으로 콘케이브가 있다. -f 가 컨벡스하다면 f는 콘케이브 하다고 말할 수 있다.

어떤 함수가 컨벡스하면서 콘케이브하다면 해당 함수는 아핀 함수이다. 아핀 함수는 컨벡스 조건 부등식을 만족하기 때문

2.2 컨벡스 함수의 예

지수 함수는 모든 실수에 대해 a 값에 관계없이 컨벡스 하다. f(x)=e^ax
절댓값 함수 f(x)=|x| 는 컨벡스하다.
멱함수 f(x)=x^a 는 a>=1 또는 a<=0이고, x>=0 일 때 콘케이브하다.
멱함수 f(x)=x^a 는 0<=a<1 이고, x>=0 일 때 콘케이브하다.
로그 함수 f(x)=logx 는 콘케이브하다.
Lp-Norm||x||_p는 컨벡스하다.

2.3 1차, 2차 미분 조건

1차 미분 조건 first-order conditions 은 최적값을 찾는 데 중요한 역할을 한다.

함수 f가 미분 가능하다는 말은 함수 f의 정의역 내 모든 점에 대해, 해당 점의 미분값, 그레이디언트가 존재한다는 뜻이다.

연속적인 그래프 형태,

f가 미분 가능하다고 할 때 함수 f가 컨벡스하다는 말은 곧 함수 f의 정의역이 컨벡스하며 위와 같은 부등식이 모든 점 x1, x2에 대해 만족하다는 말과 같다. (함수의 정의역이 컨벡스 한 것)

1차 미분 조건을 그림으로 표현

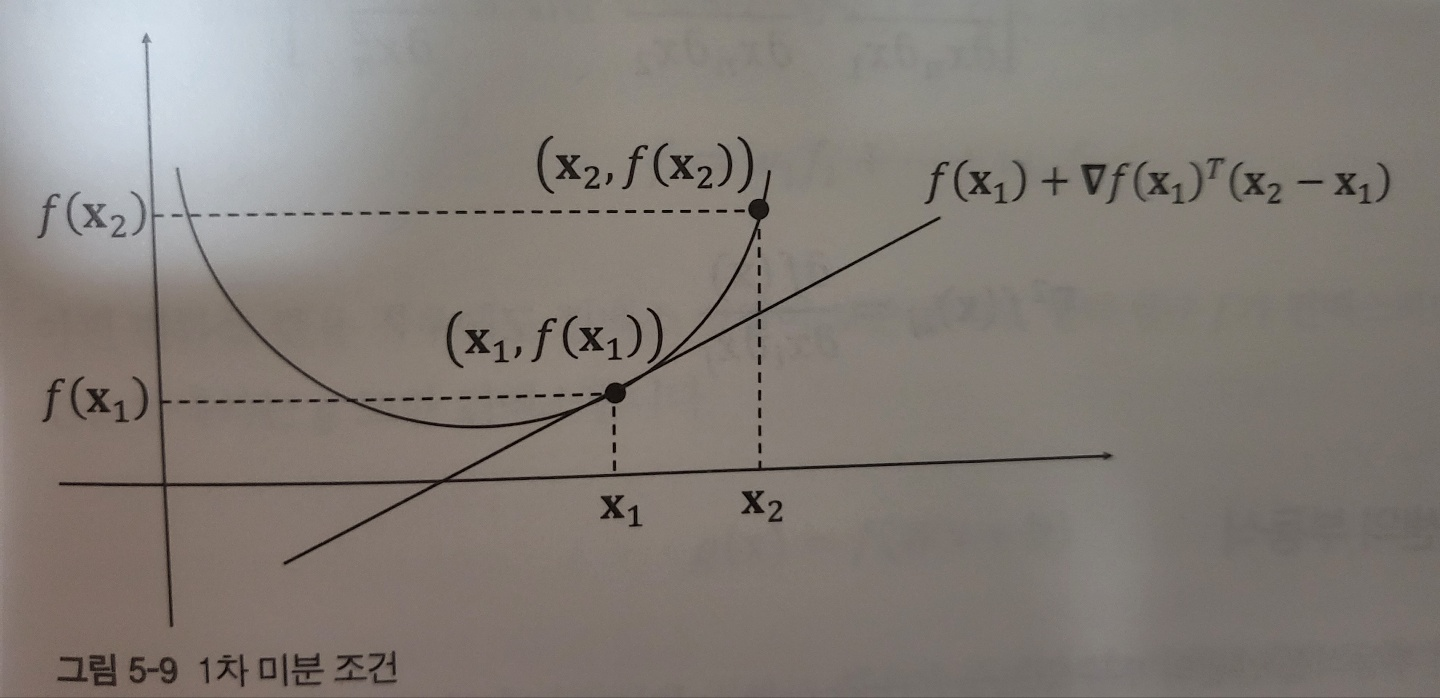
더해지는 f(x1) 값이 x2, x1 의 변화량에 대한 편향값이 되는 것,

위 부등식이 의미하는 것은 컨벡스 함수에 대해 지역 정보를 알려주며, 이로부터 전역 정보를 유도할 수 있다.

그래디언트값이 0일 때, 모든 x2∈dom f 에 대해 f(x2)>=f(x1) 이라면, x1은 함수 f에 대한 전역 최솟값이다. 왜냐하면 모든 지역에서 f(x2)는 f(x1) 보다 크거나 같기 때문이다. (이를 유도하기 위해 컨벡스하다는 개념이 등장한 것 아닐까? 그래디언트 값이 0이 되는 부분이 전역 최솟값이 되기 위한 조건을 생각했을 때)

2차 미분 조건은 함수 f가 두 번 미분 가능해서 ▽^2f 가 존재할 때, 함수 f의 정의역에 존재하는 모든 x에 대해

이면, 함수 f는 컨벡스 하다. 이는 ▽^2f의 헤시안 행렬이 준양정치행렬이라는 말과 같다. (당연한 이치, 반대의 부등호의 경우 콘케이브)

해시안 행렬 hessian matrix 이란 함수 f의 2차 미분계수를 이용해 만든 행렬을 의미한다.

2.4 얀센의 부등식

앞서 배운 부등식을 얀센의 부등식 Jansen's inequality 라고도 부른다.

좀 더 일반화시켜 나타내면 아래와 같다

이 때 , x1,...xk ∈dom f 이며, w1,...,wk >=0 이고 sum(wk)=1 이다.

얀센의 부등식을 응용해 흔히 사용되는 부등식 중 하나는 아래와 같다. 아래 부등식에서 E는 기댓값을 의미한다.

응용하여 간단한 부등식도 쓸 수 있다.

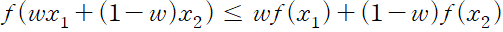
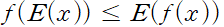
2.5 컨벡스 성질 보존 조건

컨벡스 성질이 보존되는 경우, 비음수 가중합 nonnegative weighted sums 을 적용할 때 컨벡스 성질이 보존(당연)

f1, f2가 컨벡스 할 때, 두 함수의 합 또한 컨벡스(당연)

이를 정리하면 아래 조건을 만족하는 함수 f는 컨벡스 (가중치는 0보다 크기 때문, 당연)

또한 여러 컨벡스 함수의 최댓값을 구하는 함수가 존재할 때, 최댓값 함수 또한 컨벡스 함수이다.

예를 들어 f1과 f2 모두 컨벡스 함수이고 두 함수의 최댓값 함수를 f라고 했을 때, f 역시 컨벡스 함수이다. 이를 일반화한 모습

f 가 컨벡스 함수일 때, f의 합성 함수 또한 컨벡스 함수이다.

3. 라그랑주 프리멀 함수

3.1 일반적인 최적화 문제

라그랑주 승수법 Lagrange Multiplier Method 는 제약식이 있는 최적화 문제를 푸는 방법

최적화를 하려는 값에 라그랑주 승수항을 더해 제약이 있는 문제를 제약이 없는 문제로 바꿈으로써 해결할 수 있다.

최적화를 한다는 말은 극값을 구한다는 뜻이며, 극값을 구한다는 말은 최댓값이나 최솟값을 구하는 것을 의미한다.

최적화시키려는 목적 함수는 f(x)이다. 자주 사용되는 목적 함수에는 MSE와 같은 함수가 존재한다. 이때 x는 최적화 변수고, n 차원 실수 공간에 속한다.

이를 간단히 표현하면 x∈R^n 으로 나타낸다. 구하려는 최적값을 p라고 한다. 위 식에서 g(x), h(x) 는 제약식을 나타낸다. g(x) 는 부등호를 포함하는데 이를 부등식 제약 함수라고 한다. h(x) 와 같이 등호를 포함하는 제약 함수는 등식 제약 함수라고 한다.

inequality constraint function, equality constraint function

3.2 컨벡스 최적화 문제

일반적인 최적화 형태와 컨벡스 최적화는 몇가지 조건이 추가된다. 우선 f(x), g(x) 는 모두 컨벡스 함수이어야 한다는 조건이 붙는다. 즉, 목적함수와 부등식 제약 함수가 모두 컨벡스 함수여야 한다는 뜻

등식 제약 조건 함수는 아핀 함수여야 한다.

최적화 문제에서 주목해야 할 부분은 부등식의 부호이다. 왜 함수 g(x)는 0보다 작아야 할까? 그 이유는 g(x)<=0 을 만족해야 컨벡스하기 때문이다.

만약 f(x)=x^2-1 이라는 함수가 존재하고, 제약 조건은 f(x)<=0 이라고 한다. 이 경우 x^2-1<=0 이면 이를 만족하는 변수 x의 해는 -1<=x<=1 이다. 왼쪽 그림을 보면, 해당 영역에 있는 변수는 연속이므로 제약 조건은 컨벡스하다.

반면 오른쪽의 그림은 제약 조건이 f(x)>=0 일때, x^2-1>=0 을 만족하는 해는 x>=1 또는 x<=-1 이다. 이경우 변수 x는 불연속적이다.

제약 조건 x^2-1>=0은 컨벡스하지 않는다.

3.3 라그랑주 프리멀 함수

최적화 문제를 아래와 같이 표현한 것을 라그랑지안이라고 하며, 라그랑주 프리멀 함수 Lagrange primal function 라고 한다. L_p 는 아래와 같다.

람다를 제약식 g(x)<=0 에 대한 라그랑주 승수라고 하며, vi 를 제약식 h(x) 에 대한 라그랑주 승수라고 한다.

이 두개를 듀얼 변수 또는 라그랑주 승수 벡터라고 부른다.

최적화하고 싶은 목적 함수를 f(x1,x2)=(x_1)^2+(x_2)^2 라 하고, 등식 제약 조건을 h(x,y)=x1+x2=2 라고 한다. 이때, 극값을 구하기 위한 라그랑주 프리멀 함수는 아래와 같다.

위 문제를 풀기 위해 편미분 결과가 0이 되는 지점을 찾는다.

위 식을 정리해 각 극값을 찾을 수 있다.

4. 라그랑주 듀얼 함수

라그랑주 듀얼 함수 Lagrange dual function L_D 는 라그랑주 프리멀 함수의 하한을 나타낸다.

만약 라그랑주 프리멀 함수의 하한이 없는 경우에 라그랑주 듀얼 함수는 마이너스 무한대 값을 가진다. 라그랑주 듀얼 함수는 람다>=0 에 대해 최적값 p의 하한을 나타낸다. 이를 식으로 나타내면 다음과 같다.

만약 라그랑주 듀얼 함수의 최적값을 d* 라고 하면아래와 같은 부등식이 성립한다. 즉, 프리멀 문제의 최적값을 구하는 것은 듀얼 함수를 최대화하는 것과 동일하다.

위와 같은 성질을 weak duality 라고 한다. 즉, 라그랑주 듀얼 함수의 최적값 d*는 라그랑주 프리멀 함수의 최적값 p* 보다 작거나 같다. 이 두 최적값의 차이 p*-d* 를 듀얼리티 갭 duality gap 이라고 부른다. 듀얼리티 갭은 nonegative, 0보다 크다.

만약 라그랑주 듀얼 함수의 최적값과 라그랑주 프리멀 함수의 최적값이 동일한 경우, 즉, 듀얼리티 갭이 0인 경우를 string duality 라고 부른다. d*=p*

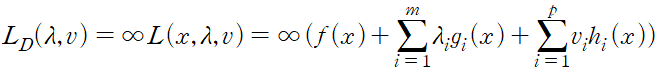
5.Karush-Kuhn-Tucker 조건

프리멀 문제가 컨벡스할 때, KKT 조건을 이용하면 프리멀 최적값임과 동시에 듀얼 최적값임을 보일 수 있다. 이를 프리멀 듀얼 최적화라고 한다.

즉 f,g 가 컨벡스 함수이고

6. 머신러닝에서의 최적화 문제

최소 제곱법

제약식이 추간된 최소 제곱법

7. 뉴턴-랩슨 메소드

이론적으로 해를 구하기 어려운 경우가 많다. 이 때 해의 근삿값을 구한다. 뉴턴-랩슨 메소드(Newton-Raphson method)는 함수의 해의 근삿값을 구할 때 사용하는 방법이다.

초깃값을 기준으로 아래의 식을 반복하여 해를 구한다.

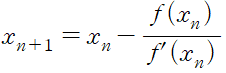
그림에서 구하려는 최적값을 p*=x* 라고 할 때, 초깃값을 x1 이라고 한다. 그러면 초깃값에 대한 함수값 f(x1)을 구할 수 있으며 해당 점에서의 기울기를 구할 수 있다. 그리고 해당 접선과 x추기 만나는 지점을 x2라고 한다. 이와 같은 과정을 반복하여 최적해의 근삿값을 구할 수 있다.

8 그래디언트 디센트 옵티마이저

8.1 그래디언트 디센트 소개

실제로 머신러닝 알고리즘을 사용할 때 옵티마이저는 최적화 목적 함수인 손실 함수를 기반으로 매 학습 때 어떻게 업데이트할지를 결정한다.

그래디언트 디센트는 비용 함수의 미분값을 이용하는 방법이다. 미분해서 0이되는 최적값을 탐색하는 방법으로 최초에 구한 미분값의 반대 방향으로 이동시킨 후, 이동한 지점에서 다시 미분을 한다. 이러한 과정의 반복으로 최적값에 가까워진다.

구하려는 모형의 파라미터를 a 라고 하고, 목적 함수를 J(a) 라고 하면 그레이언트 디센트는 아래와 같은 과정을 거친다.

그래디언트 디센트

초기 파라미터 a1 에 해당하는 J(a1)의 미분값을 구한다.
1에서 구한 미분값의 반대 방향으로 a1를 ▽J(a1)만큼 이동시킨다. 이동 후 지점을 a2라고 한다.
1,2 단계를 반복한다.

위 그래디언트 과정의 수식 표현

미분값의 반대 방향으로 이동시ㅣ므로 마이너스 부호가 붙는다. 이때 학습률의 개념을 사용, 너무 많이 이동하지 않도록 하기 위한 파라미터

미분값, 변화량

8.2 확률적 그래디언트 디센트

트레이닝 데이터 전체에 대해 그래디언트 디센트를 수행하는 것을 배치 그래디언트 디센트라고 하고 데이터 크기가 큰 경우 계산의 시간이 길어진다.

이러한 단점을 보완하기 위해 전체 데이터에서 추출한 샘플 트레이닝 데이터를 사용한 확률적 그레디언트 디센트를 사용해 최적값을 찾는다.

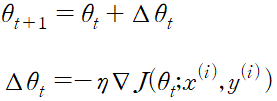
수렴속도가 빠른 만큼 최적해를 벗어나느 경우도 존재, 때문에 학습률을 더 낮춘다.

위 두가지를 보완한 것이 미니 배치 그레디언트 디센트 mini-batch gradient descent

i번째 데이터 포인트부터 i+n 데이터 포인트를 포함한다는 뜻

8.3 모멘텀

학습 속도를 가속화하는 방법으로 모멘텀 momentum 이 존재

모멘텀 하이퍼파라미터 r은 모멘텀을 얼마나 줄 지 결정하는 값으로 0.9 근방의 값으로 설정된다. 위 두 식을 더해 하나의 식으로 표현

그레디언트 최적화와 비교,

기존 SGD보다 학습 속도가 rv_t-1 만큼 가속한다. 이때 v_t 는 이동 벡터로 아래와 같이 구할 수 있다.

이전 파라미터들에 대해 더해진다.

한 스텝, 스텝이 커진다

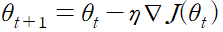
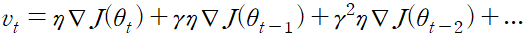
8.4 네스테로프 가속 경사 (Nesterov Accelerated Gradient)

모멘텀을 기반으로 하는 방법 모멘텀에서는 파라미터가 rv_t-1 만큼 이동, 대략적인 다음 시점의 파라미터 위치를 추정할 수 있다.

이를 이용한 방법이 네스테로프 가속 경사 NAG Nesterov Accelerated Gradient 이다.

목적 함수에 쓰이는 파라미터 값이 다음 시점의 파라미터이다. (이해 완료)

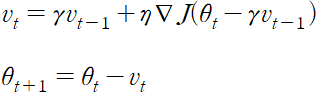
8.5 Adagrad

최적값을 구하려는 각 파라미터의 중요도에 따라 각기 다르게 학습률을 적용하는 방법, 매 시점의 개별 파라미터 a에 대해 서로 다른 학습률을 적용한다.

g_t,i 는 시점 t에서 i번째 파라미터 ai 에 대해 적용할 그래디언트를 의미, 파라미터 a에 대해 다음과 같이 업데이트 한다.

모든 타임 스텝 t에 대해 ai를 업데이트하면 아래와 같다.

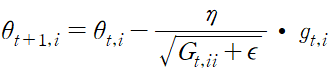
엡실론은 분포가 0이 되는 것을 방지하기 위한 겂, G_t는 대각 행렬로 각 대각 원소는 at의 과거 그래디언트의 제곱합이다.Gt는 아래와 같은 방법으로 구할 수 있다.

전체 파라미터 식으로표현,

8.6 Adadelta

Adagrad 의 확장된 개념, Adagrad 에서는 과거 모든 시점의 그래디언트 제곱합을 더했는데, Adadelta 에서는 과거 모든 시점의 그래디언트 제곱합을 더하는 대신, 과거 그래디언트를 더하는 시점을 고정한다. 최근 시점의 그래디언트를 이용해 파라미터 값을 추정하는 방법

장점은 학습 횟수가 많이 반복되어도 계속해서 개선 의지가 있다는 장점이 있다.

특정 과거 시점을 지정하는 대신 그래디언트 제곱의 지수적 감소 평균을 사용한다. exponentially decaying average of the squared gradient, t시점에서의 해당 값은 E(g^2)_t 라고 표현

위 공식에서 r은 모멘텀에서의 r, 0.9 근방의 값

파라미터 업데이트는 Adagrad 에서 사용했던 term 과 비슷, 대각 행렬 G_t를 과거 그래디언트 제곱 감소 평균으로 변경

위 식에서 분모를 보면 RMSE 라는 것을 알 수 있다.

8.7 RMSprop

Adadelta 와 비슷, 차이점은 학습률의 사용 여부, RMSprop 에서는 학습률을 사용한다.