설정하기 어려운 hyper parameter 로 learning rate, 모형의 성과에 영향을 미치기 때문, 비용 함수는 일부 방향으론 민감하게 반응하지만, 그 외의 방향에서는 아주 둔감하다.
운동량 알고리즘으로 어느 정도 완화할 수 있지만, 또 다른 초매개변수를 도입해야 한다는 점,
민감도의 방향들이 공간의 축에 어느 정도 정렬되어 있다고 가정한다면, 매개변수마다 개별적인 학습 속도를 두고 학습 과정에서 그 학습 속도들을 자동으로 적응시키는 방법이 합당할 것,
훈련 도중 개별 학습 속도를 모형 매개변수들에 적응시키는 발견법적 접근 방식으로는, delta-bar-delta 라는 알고리즘이 제시된 바 있음, 만일 손실함수의 주어진 모형 매개변수에 대한 편미분의 부호가 바뀌지 않았다면 학습 속도를 증가하고, 부호가 바뀌었다면 학습 속도를 감소해야 한다. 라는 간단한 착안에 기초,
모형 매개변수의 학습 속도를 적응적으로 변화시키는 여러 점진적인 방법들이 제시
AdaGrad
- 적응형 학습률 : 각 파라미터에 대해 학습률을 개별적으로 조정, 학습률은 이전 기울기들의 제곱합에 따라 조정
- 희소 데이터 처리 유리 : sparse update parameter 는 학습률이 크게 유지되어 충분히 학습 가능,
- 감소하는 학습률 : 학습이 진행됨에 따라 학습률이 감소, 나중에는 학습이 거의 이뤄지지 않을 수 있음
업데이트 공식

RMSProp
AdaGrad 의 수정, 기울기 누적 대신 지수 가중 이동 평균 exponentially weighted moving average 의 사용
- 지수 가중 이동 평균 : 과거 기울기의 제곱합을 지수적으로 감소, 현재 기울기 누적, 학습률이 작아지지 않도록
- 적응형 학습률 : 각 파라미터에 대해 개별적으로 학습률을 조정
- 안정된 학습 : 학습 과정에서 기울기의 변화에 더 민감하게 반응하면서도 안정성 유지
RMSprop 의 업데이트 공식

beta 는 지수 가중 이동 평균의 감쇠율,
기울기의 변화에 더 민감하게 반응하면서도, 학습률이 너무 빠르게 감소하지 않도록 한다. 안정적이고 효율적인 학습을 보장
Exponentially Weighted Moving Average, EWMA
최근의 데이터에 더 큰 가중치 부여, 평균 계산, 최근 데이터가 과거 데이터보다 더 중요한 경우에 유용,
각 데이터 포인트에 가중치를 지수적으로 감소시켜 적용
EWMA 계산 공식
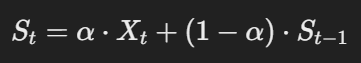

가중치 계수 alpha, 최근 데이터를 얼마나 더 중요시할 것인지를 결정,
Adam, adaptive moments
RMSProp 와 Momentum 의 장점을 결합한 최적화 알고리즘, 학습률을 적응형으로 조정하면서도, 과거의 기울기와 기울기의 제곱을 모두 고려하여 더욱 효율적이고 안정적인 학습의 제공
- 적응형 학습률 : 각 파라미터에 대해 학습률을 개별적으로 조정
- 1차 및 2차 momentum 사용
- bias 보정 : 초기 단계에서 모멘트 추정치의 bias 를 보정하여 더 정확한 업데이트의 제공

beta_1,2 는 각각 1, 2 차 모멘트의 지수 가중 이동 평균의 감쇠율,
알고리즘 선택 문제는 사용자가 주어진 알고리즘에 얼마나 익숙한가에 크게 의존
'ml_interview' 카테고리의 다른 글
| 운동량, momentum (0) | 2024.08.07 |
|---|---|
| 경사 하강법 기본 알고리즘 (0) | 2024.08.07 |
| Support Vector Machine, kernel 기법이 뭔데 그래서 (0) | 2024.08.06 |
| 손실 함수 최소화? 그거 아닌데!! - 데이터 생성 분포에 대한 일반적 손실 최소화 (0) | 2024.08.01 |
| 반복 재가중 최소 제곱법, Iterative Reweighted Least Squares (0) | 2024.08.01 |

