일반화 성능을 높이기 위해 훈련 오차가 증가하더라도 시험 오차를 줄이려는 전략, 정칙화 - regularization
정칙화의 방법
- 기계 학습 모형에 추가적인 제약을 도입하는 전략,
- 목적함수(비용함수라고 생각하면 될 듯) 에 새로운 항을 추가하는 전략
정칙화의 이유
- 때에 따라서는 구체적인 종류의 사전 지식을 부호화하기 위해 제약과 벌점을 고안하기도 한다.
- 더 단순한 모형으로의 일반적인 선호도를 지정하려는 의도록 제약들과 벌점을 설계하는 경우
- underdetermined 문제를 결정 문제로 바꾸기 위해 ( 특정 조건 내 최적의 해 선택 )
매개변수 노름 벌점
목적함수 J (최소화하거나 최대화하려는 함수를 의미, 회귀 분석에서는 잔차 제곱합을 최소화하는 것이 목적함수 -> 비용함수) 에 매개변수 노름 벌점 parameter norm panalty 를 추가해, 모형의 수용력을 제한,
정칙화가 가해진 목적함수 J~

- lambda >= 0, 노름 벌점 항
- OMEGA의 상대적인 기여도를 결정하는 가중치로 작용하는 hyper parameter
정칙화된 목적함수 J~ 를 훈련 알고리즘이 최소화 시, J 와 매개변수들, theta 의 크기에 대한 어떤 측도가 감소하게 된다. OMEGA 의 선택에 따라 선호되는 해의 특성이 달라진다. (L1, L2 , ... )
일반적으로 신경망에서는 affine translation (linear transformation - weight, translate - bias, 를 결합한 수학적 변환)에서 W 에만 벌점, 정칙화을 가하고, bias 는 정칙화를 수행하지 않음 (bias 는 모델의 출력을 조절, 이러한 유연성을 불필요하게 제한하므로)
대체로 bias 는 weights 보다 더 적은 양의 자료로도 정확하게 적합시킬 수 있다.
weight 는 두 변수의 상호 작용 방식을 결정하기 때문에 가중치를 잘 적합시키기 위해서는 다양한 조건들에서 두 변수를 관측할 필요가 있지만, bias 는 하나의 변수만 제어 - 이를 정칙화하지 않아도 분산이 아주 커지지 않음
bias 의 정칙화 시 under fitting 이 크게 발생할 수 있음
신경망의 맥락에서는 각 층의 서로 다른 lambda 계수에 대해 개별적인 벌점을 사용하는 것이 바람직 할 때가 존재, 이는 계산 비용이 크므로 동일한 가중치 감쇄를 사용함으로써 검색 공간의 크기를 줄이는 것도 합리적
L2 매개변수 정칙화
가장 많이 쓰이는 매개변수 노름 벌점, L2, weight decay 가 이 벌점을 사용하는 정칙화 전략,
목적함수에 정칙화 항을 추가, 가중치들을 원점에 가까운 쪽으로 이동시킨다.

bias 를 제외한 모형의 목적함수

자기 자신의 내적과 L2 노름은 동일
위 매개변수 기울기

가중치를 갱신, 한 번의 기울기 단계 식

우변의 전개

위 식을 통해 알 수 있는 것은,
 정규화 항이 없는 목적함수의 가중치 갱신 단계 |
 L2 정규화 항이 추가된 목적함수의 가중치 갱신 단계 |
정규화 항이 없는 식과 정규화 항이 있는 가중치 갱신 단계의 비교,
가중치 감쇄 항을 더하고난 후 한번의 가중치 갱신 단계에서 가중치 벡터가 상수 계수에 비례해서 줄어드는 형태로 학습 규칙이 바뀌는 것을 볼 수 있다. (상수 계수 = learning_rate * 정규화 상수 값, lambda)
좀 더 단순한 분석을 위해, 정칙화되지 않은 훈련 비용이 최소화되는 가중치 값들인 w* = argmin_w J(w) 의 부근에서 목적함수를 이차 함수로 근사, 목적 함수가 실제로 이차함수이면 이러한 근사는 완벽하다. 근사된 목적함수 J^
w* : 비용 함수가 최소가 되는 w 값

w* 의 비용 함수가 최소가 되는 값으로 인해 두 번째 항은 0으로 바뀜, - 일차 항이 없다.
H 는 목적 함수의 Hessian matrix, w* 에서의 이차 미분값의 포함들이 포함된 행렬
1. 헤시안 행렬과 극소점
목적함수 J(w) 의 w 에 대한 이차 미분으로 구성된 행렬이 헤시안 행렬 H, 이 행렬은 함수의 곡률 cuvature 정보를 담고 있으며, 주어진 점에서의 함수 오목성 convexity 또는 볼록성을 판단하는 데 사용된다.
헤시안 행렬, H 의 성질은 w* 에서 J(w) 의 극소점 여부를 결정하는 중요한 요소이다.
- 양의 준정부호 : H 가 positive semi-definite 라면, w* 는 극소점일 수 있다. J(w) 는 w* 부근에서 최소값을 가지거나 평평할 수 있다. v^T H v >= 0 이 성립하는 경우
2. 극소점에서의 헤시안의 역할
- 극소점 : w* 가 극소점이라면, 목적함수의 기울기 d J(w*) = 0 이다. 하지만 함수가 실제로 극소점인지 확인하려면, 그 점에서의 곡률 정보를 확인해야 하며, 곡률 정보는 헤시안 행렬 H 에 의해 제공된다.
- 양의 준정부호 조건 : H 가 양의 준정부호라면, w* 에서 함수가 최소화될 수 있음을 보장한다.

위 식은 이차 함수 근사에서 흔히 사용되는 표현, 이 식을 통해 목적 함수의 기울기와 헤시안 행렬의 관계를 설명할 수 있다. 특히 J(w) 가 이차 함수로 근사될 수 있는 상황에서 유용하다.
구성 요소
기울기 : 매개변수 w 에 대한 일차 미분 벡터, 해당 벡터는 J(w) 가 가장 가파르게 증가하는 방향
헤시안 행렬 : 매개변수에 대한 이차 미분으로 구성된 대칭 행렬, 함수의 곡률
w - w* : 현재의 가중치 w 와 목적함수의 극소점 w* 간의 차이를 나타낸다. w 는 현재 탐색 중인 매개변수 벡터, w* 는 목적함수를 최소화하는 매개변수 벡터
이차 함수 근사
목적 함수 J(w) 가 최소화 지점 w* 부근에서 이차 함수로 근사될 수 있다고 가정하면, 이차 함수 근사의 표현

J(w*) 은 최소화 지점에서의 목적함수 값, 3번째 항은 w 와 w* 사이의 거리와 H 에 의해 가중된 이차 항
기울기와 헤시안의 관계
위 식에서 w 에 대한 기울기를 계산 시

w* 에서 w 로 얼마나 떨어져 있는지를 H 에 의해 가중합하여 나타낸 것
두 변수의 사이가 멀어질수록 기울기의 크기는 헤시안에 의해 조정된다.
다시 돌아와서 위 식에 가중치 감쇄를 추가





헤시안 행렬이 다음의 특징, 실수 대칭 행렬, 다음의 특징이 있음
- Symmetic matrix 의 eigenvalue 는 실수이다.
- eigenvector 는 서로 직교한다.
- eigenvector 로 이루어진 행렬 Q 는 othogonal matrix 로 Q^T Q = I 를 만족한다.
다음의 형태로 고윳값 분해 가능

이 분해를 다음 식에 적용


가중치 감쇄 항은 w* 를 H 의 고유벡터들로 정의된 축들을 따라 rescaling 하는 효과를 낸다.
H 의 고윳값이 큰 방향(가중치)들에 대해서는 정칙화의 효과가 낮고, 작은 성분들은 크기가 0에 가까워질정도로 줄어든다.
목적함수의 감소에 기여하지 않는 방향들에서는 헤세 행렬의 고윳값이 작다. 이는 그 방향으로 이동해도 기울기가 크게 증가하지 않음을 의미, 중요하지 않은 방향들에 해당하는 가중치 벡터 성분들은 훈련 과정에서 정칙화에 의해 점차 감소

L2 regularization 이 최적의 가중치 w 에 미치는 영향을 설명
- 타원형 등고선
- 그래프의 중심에서 바깥쪽으로 퍼져나가는 타원형 등고선들은 목적 함수 J(w) 의 등고선을 나타낸다. 이는 주어진 문제에서 손실 함수의 값이 동일한 지점을 연결한 선들
- 이는 목적 함수가 특정 지점, w* 에서 최소화된다는 것이다. 즉, w* 는 정칙화가 없는 경우, 목적 함수의 최적의 가중치값이다.
- 동심원 형태의 점선
- L2 regularization 항 lambda w^T w 의 등고선을 나타낸다. 이는 가중치 w 의 크기를 제한하는 효과를 시각화한 것이다.
- w가 원점에서 멀어질수록 정칙화 항이 증가함을 나타낸다. 정칙화는 가중치 w 의 크기를 작게 유지하려고 한다.
- 최적화된 가중치 w~
- 이 점은 손실 함수와 정칙화 항의 결합된 함수가 최소화되는 지점
선형 회귀에서 L2 regularization 가 적용된 해의 표준 방정식
 |
 |
| 정칙화 x | 정칙화 o |
정칙화 x 의 행렬 X^T X 는 공분산 행렬 1/m X^T X 에 비례한다.
L2 regularization 을 적용하면 이 값이 대체된다.
이 새 행렬은 원래의 행렬의 대각 성분들에 lambda 값을 더한 것, 이 행렬의 대각 성분들은 각 입력 특징의 분산에 해당한다.
따라서 L2 regularization 은 학습 알고리즘이 입력 X 의 분산을 실제보다 더 높다고 느끼게 만든다. 결과적으로 학습 알고리즘은 출력 목표와의 공분산이 그러한 증가된 분산보다 낮은 특징들에 대한 가중치를 감쇄하게 한다.
- 모델이 큰 가중치를 할당하는 것을 피하기 위해 작은 가중치 값을 선택, 결과적으로 특정 입력 특징이 출력 목표와 강하게 연관되어 있지 않다고 느끼게 됨
- 이는 모델이 특정 입력 특징 X 와 출력 목표 y 사이의 상관관계, 공분산 covariance 가 감소된 것처럼 느끼게 만든다.
모델은 입력 특징 X 와 출력 목표 y 사이의 공분산이 낮은 특징에 대해 더 작은 가중치를 할당하게 된다. 반면, 출력과 강하게 상관된 특징, 공분산이 높은 특징들에 대해서는 상대적으로 더 큰 가중치가 유지된다. 중요하지 않은 특징들에 대해 높은 가중치를 할당하는 것을 방지
L1 Regularization
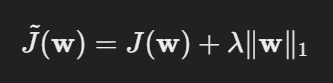
L1 regularizatoin 이 포함된 목적 함수의 기울기 벡터 식

불연속적인 형태, 때문에 이차 근사에 대한 대수적 해가 존재하지 않는다.
이를 보장하기 위해 H 가 반드시 대각 행렬이어야 하나는 가정 추가, 이 가정은 입력 특징들 사이의 상관관계를 모두 제거했을 경우 성립 - PCA 를 통해 수행 가능

행렬 곱의 형태를 가중치 각 성분, w_i 의 합으로 분리
이 근사 비용함수를 최적화하는 문제에는 해석적 해가 존재,

w_i 의 부호, 1, -1
0 보다 작을 경우 0,
w_i 가 lambda 보다 작으면 최적의 w_i 는 0이 된다.
lambda 보다 클 경우 w_i 에서 lambda 만큼 감쇠된 값을 갖는다.
L1 regularization 은 sparse 해를 산출한다. lambda 가 충분히 크다면 매개변수들이 희소해질 수 있음을 보여준다. 이러한 특징으로 특징 선택의 메커니즘으로 활용 가능 ( 임의 개수의 w 를 0으로 만들기 위한 lambda 값의 범위도 계산할 수 있을 것이다.)
'ml_interview' 카테고리의 다른 글
| 데이터 증강 augmentataion 과 모델 훈련, (0) | 2024.08.22 |
|---|---|
| regularization and underdetermined, 반복 최적화의 알고리즘은 w의 크기를 무한정 증가시킨다. , pseudoinverse 와 regularization 의 관계 (0) | 2024.08.22 |
| 흔히 쓰이는 확률분포 - 주어진 분산을 가지는 모든 가능한 연속 확률 분포 중에서 가장 많은 불확실성을 부호화하는 것이 정규 분포라는 사실은 매우 중요한 통계적 성질 (0) | 2024.08.20 |
| 확률론과 정보 이론 (0) | 2024.08.20 |
| Marginal Distribution, 주변 분포 (0) | 2024.08.07 |


