훨씬 더 깊은 심층 신경망을 훈련할 경우 문제를 마주할 수 있다.
- 그레이디언트 소실, 그레이디언트 폭주 문제에 직면할 수 있다. 신경망의 아래쪽으로 갈수록 그레이디언트가 점점 더 작아지거나 커지는 현상, 하위층을 훈련하기 매우 어렵게 만든다.
- 훈련 데이터가 충분하지 않거나 레이블을 만드는 작업에 비용이 많이 든다.
- 훈련이 극단적으로 느려질 수 있다.
- 수백만 개의 파라미터를 가진 모델은 훈련 세트에 과대적합될 위험이 매우 크다. 특히 훈련 샘플이 충분하지 않거나 잡음이 많은 경우 그렇다.
11.1 그레이디언트 소실과 폭주 문제
역전파 알고리즘은 출력층에서 입력층으로 오차 그레이디언트를 전파하면서 진행된다. 알고리즘이 신경망의 모든 파라미터에 대한 오차 함수의 그레이디언트를 계산하면서 경사 하강법 단계에서 이 그레이디언트를 사용하여 각 파라미터 수정한다.
알고리즘이 하위층으로 진행될수록 그레이디언트가 점점 작아지는 경우가 많다. 이를 그레이디언트 소실 vanishing gradient 반대로 그레이디언트가 점점 커져서 여러 층이 비정상적으로 큰 가중치로 갱신되면 알고리즘은 발산 diverse 한다. 이를 그레이디언트 폭주 exploding gradient 라고 하며 순환 신경망에서 주로 나타난다. 불안정한 그레이디언트는 심층 신경망 훈련을 어렵게 만든다. 층마다 학습 속도가 달라질 수 있기 때문
그레이디언트가 불안정해지는 원인으로 로지스틱 시그모이드 활성화 함수와 가중치 초기화 방법(평균이 0이고 표준편차가 1인 정규분포)의 조합이었다. 이 활성화 함수와 초기화 방식을 사용했을 때 각 층에서 출력의 분산이 입력의 분산보다 더 크다는 것을 밝혔다. 신경망의 위쪽으로 갈수록 층을 지날 때마다 분산이 계속 커져 가장 높은 층에서는 활성화 함수가 0이나 1로 수렴한다. 이는 로지스틱 함수의 평균이 0.5라는 사실 때문에 더 나빠진다.
로지스틱 함수는 항상 양수를 출력하므로 출력의 가중치 합이 입력보다 커질 가능성이 높다. 이를 편향 이동 bias shift 라고도 부른다

로지스틱 활성화 함수를 보면 입력이 커지면 0이나 1로 수렴해서 기울기가 0에 매우 가까워진다. 그래서 역전파가 될 때 신경망으로 전파할 그레이디언트가 거의 없고 조금 있는 그레이디언트는 최상위층에서부터 역전파가 진행되면서 점차 약해져 아무것도 도달하지 않게 된다.
11.1.1 글로럿과 He 초기화
예측을 할 때는 정방향으로, 그레이디언트를 역전파할 때는 역방향으로 양방향 신호가 적절하게 흘러야 한다. 신호가 죽거나 폭주 또는 소실하지 않아야 한다. 적절한 신호가 흐르기 위해서는 각 층의 출력에 대한 분산이 입력에 대한 분산과 같아야 한다고 주장했다.(글로럿과 벤지오)
그리고 역방향에서 층을 통과하기 전과 후의 그레이디언트 분산이 동일해야 한다.
사실 층의 입력과 출력 연결 개수가 같지 않다면 이 두 가지를 보장할 수 없다. 하지만 대안이 제안됨, 각 층의 연결 가중치를 무작위로 초기화하는 것이다. 이 초기화 전략을 세이비어 초기화 혹은 글로럿 초기화라고 한다.

케라스는 기본적으로 균등분포의 글로럿 초기화를 사용한다.
11.1.2 수렴하지 않는 활성화 함수
활성화 함수를 잘못 선택하면 그레이디언트의 소실이나 폭주로 이어질 수 있다. 이전에는 시그모이드 활성화 함수가 최상의 선택일 것이라고 생각했다. 하지만 다른 활성화 함수의 등장
특히 ReLU 함수가 심층 신경망에서 훨씬 더 잘 작동한다 특정 양숫값에 수렴하지 않고 계산도 빠르다. 하지만 훈련하는 동안 일부 뉴런이 0 이외의 값을 출력하지 않는다.
이 문제를 해결하기 위해 LeakyReLU의 함수의 변종을 사용한다. 하이퍼파라미터 a가 이 함수가 새는 정도를 결정 z < 0 일 때의 기울기를 설정한다.
훈련하는 동안 a를 무작위로 선택하고 테스트시에는 평균을 사용하는 RReLU, a가 훈련하면서 학습되는 PReLU도 존재,

ELU의 새로운 활성화 함수의 등장, 다른 모든 ReLU 변종의 성능을 앞질렀다. 훈련 시간도 줄고 신경망의 테스트 세트 성능도 더 높다.

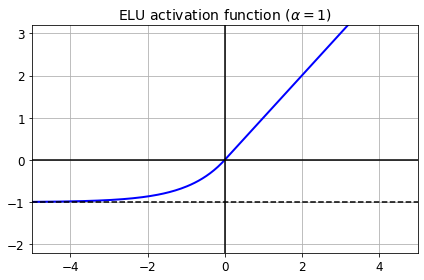
- z < 0일 때 음숫값이 들어오므로 활성화 함수의 평균 츨력이 0에 더 가까워진다. 이는 그레이디언트 소실 문제를 완화해준다. 하이퍼파라미터 a는 z가 큰 음숫값일 때 ELU가 수렴할 값을 정의한다. 보통 1로 설정
- z < 0이어도 그레이디언트가 0이 아니므로 죽은 뉴런을 만들지 않는다.
- a=1 이면 함수는 z=0에서 급격히 변동하지 않으므로 z=0을 포함해 모든 구간에서 매끄러워 경사 하강법의 속도를 높여준다.
ELU 활성화 함수의 주요 단점은 계산이 느리다는 것 훈련하는 동안 수렴 속도가 빨라서 느린 계산이 상쇄되지만 테스트 시에는 ELU를 사용한 네트워크가 ReLU를 사용한 네트워크보다 느릴 것이다.
SELU 활성화 함수는 스케일이 조정된 ELU 활성화 함수의 변종이다. 완전 연결 층만 쌓아서 신경망을 만들고 모든 은닉층이 SELU 활성화 함수를 사용한다면 네트워크가 자기 정규화가 된다. 훈련하는 동안 각 층의 출력이 평규 0과 표준편차 1을 유지하는 경향이 있어 그레이디언트 소실, 폭주를 막아준다.
그 결과로 뛰어난 성능을 보이지만, 몇 가지 조건이 있다.
- 입력 특성이 반드시 표준화되어야 한다.
- 모든 은닉층의 가중치는 르쿤 정규분포 초기화로 초기화되어야 한다.
- 네트워크는 일렬로 쌓은 층으로 구성되어야 한다.
일반적으로 SELU > ELU > LeakyReLU > ReLU > tanh > 로지스틱 순으로 활성화 함수 사용, 네트워크가 자기 정규화되지 못하는 구조라면 ELU가 더 나을 수 있다. 실행 속도가 중요하다면 LeakyReLU를 선택할 수 있다.
LeakyReLU 활성화 함수를 사용하려면 LeakyReLU 층을 만들고 모델에서 적용하려는 층 뒤에 추가한다.
model = keras.models.Sequential([
...
keras.layers.Dense(10, kernel_initializer="he_normal"),
keras.layers.LeakyReLU(alpha=0.2),
])11.1.3 배치 정규화
그레이디언트 소실과 폭주 문제를 해결하기 위한 배치 정규화 Batch Normalization 각 층에서 활성화 함수를 통과하기 전이나 후에 모델에 연산을 추가 이 연산은 입력을 원점에 맞추고 정규화한 다음 각 층에서 두 개의 새로운 파라미터로 결괏값의 스케일을 조정하고 이동 하나는 스케일 조정에, 다른 하나는 이동에 사용한다. 많은 경우 신경망의 첫 번째 층으로 배치 정규화를 추가하면 훈련 세트를 표준화할 필요 없이 배치 정규화 층이 이런 역할을 대신한다.
입력 데이터를 원점에 맞추고 정규화하려면 알고리즘은 평균과 표준편차를 추정해야 한다. 이를 위해 현재 미니배치에서 입력의 평균과 표준편차를 평가한다.

- u_B 는 미니배치 B에 대해 평가한 입력의 평균 벡터이다.(입력마다 하나의 평균을 가진다)
- a_B도 미니배치에 대해 평가한 입력의 표준편차 벡터이다.
- m_B는 미니배치에 있는 샘플 수이다.
- ^x^(i)는 평균이 0이고 정규화된 샘플 i의 입력이다.
- r 은 층의 출력 스케일 파라미터 벡터이다.(입력마다 하나의 스케일 파라미터가 있다.)
- 원소별 곱셈이다. (각 입력은 해당되는 출력 스케일 파라미터와 곱해진다.)
- B는 츠으이 출력 이동 파라미터 벡터이다.(입력마다 하나의 스케일 파라미터가 있다.) 각 입력은 해당 파라미터만큼 이동한다.
- e는 분모가 0이 되는 것을 막기 위한 작은 숫자이다.
- z^(i) 는 배치 정규화 연산의 출력이다. 즉, 입력의 스케일을 조정하고 이동시킨 것이다.
훈련하는 동안 배치 정규화는 입력을 정규화한 다음 스케일을 조정하고 이동시킨다.
테스트 시에는 샘플의 배치가 아니라 샘플 하나에 대한 예측을 만들어야 한다. 이 경우 입력의 평균과 표준편차를 계산할 방법이 덦다. 샘플의 배치를 사용한다고 하더라도 매우 작거나 독립 동일 분포 조건을 만족하지 못할 수 있다 이런 배치 샘플에서 계산한 통계는 신뢰도가 떨어진다
한 가지 방법은 훈련이 끝난 후 전체 훈련 세트를 신경망에 통과시켜 배치 정규화 층의 각 입력에 대한 평균과 표준편차를 계산하는 것이다. 예측할 때 배치 입력 평균과 표준편차로 이 최종 입력 평균과 표준편차를 대신 사용할 수 있다.
그러나 대부분 배치 정규화 구현은 층의 입력 평균과 표준편차의 이동 평균을 사용해 훈련하는 동안 최종 통계를 추정한다.
케라스의 BacthNormalization 층은 이를 자동으로 수행한다.
정리하면 배치 정규화 층마다 네 개의 파라미터 벡터가 학습된다. r(출력 스케일 벡터), B(출력 이동 벡터)는 일반적인 역전파를 통해 학습된다. u(최종 입력 평균 벡터)와 a(최종 입력 표준편차 벡터)는 지수 이동 평균을 사용하여 추정된다. u와 a는 훈련하는 동안 추정되지만 훈련이 끝난 후에 사용된다.
실험한 모든 심층 신경망에서 배치 정규화가 성능을 크게 향상시킨다는 것을 보였다. 이미지넷 분류 작업에서 큰 성과를 냈다. 그레이디언트 소실 문제가 크게 감소하여 하이퍼볼릭 탄젠트나 로지스틱 활성화 함수 같은 수렴성을 가진 활성화 함수를 사용할 수 잇다. 또 가중치 초기화에 네트워크가 훨씬 덜 민감해진다. 또한 훨씬 더 큰 학습률을 사용하여 속도를 크게 높일 수 있었다.
마지막으로 배치 정규화는 규제와 같은 역할을 하여 다른 규제 기법의 필요성을 줄여준다.
그러나 배치 정규화는 모델의 복잡도를 키운다. 실행 시간 면에서도 손해이다. 층마다 추가되는 계산이 신경망의 예측을 느리게 한다. 다행히 훈련이 끝난 후 이전 층과 배치 정규화 층을 합쳐 실행 속도 저하를 피할 수 있다. 이전 층의 가중치를 바꾸어 바로 스케일이 조정되고 이동된 출력을 만든다.
예를 들면 이전 층이 XW + b를 계산하면 배치 정규화 층은 ~ 을 계산한다. ~~
따라서 이전 층의 가중치와 편향을 업데이트된 가중치와 편향으로 바꾸면 배치 정규화층을 제거할 수 있다.
케라스로 배치 정규화 구현
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28,28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, activation="elu", kernel_initializer="he_normal"),
keras.layers.BatchNormalization(),
keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal"),
keras.layers.BatchNormalization(),
keras.layers.Dense(10, activation="softmax")
])
model.summary()
>>>
Model: "sequential_4"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
flatten_4 (Flatten) (None, 784) 0
_________________________________________________________________
batch_normalization (BatchNo (None, 784) 3136
_________________________________________________________________
dense_212 (Dense) (None, 300) 235500
_________________________________________________________________
batch_normalization_1 (Batch (None, 300) 1200
_________________________________________________________________
dense_213 (Dense) (None, 100) 30100
_________________________________________________________________
batch_normalization_2 (Batch (None, 100) 400
_________________________________________________________________
dense_214 (Dense) (None, 10) 1010
=================================================================
Total params: 271,346
Trainable params: 268,978
Non-trainable params: 2,368
_________________________________________________________________은닉층의 활성화 함수 전이나 후에 BatchNormalization 층을 추가하면 된다.
여기서 볼 수 있듯이 배치 정규화 층은 입력마다 네 개의 파라미터를 추가한다.
이 파라미터는 역전파로 학습되지 않기 때문에 케라스는 'Non-trainable' 파라미터로 분류한다.
첫 번째 배치 정규화 층의 파라미터를 살펴본다. 두 개는 역전파로 훈련되고 두 개는 훈련되지 않는다.
bn1 = model.layers[1]
[(var.name, var.trainable) for var in bn1.variables]
>>>
[('batch_normalization/gamma:0', True),
('batch_normalization/beta:0', True),
('batch_normalization/moving_mean:0', False),
('batch_normalization/moving_variance:0', False)]배치 정규화 논문의 저자들은 활성화 함수 이후보다 이전에 배치 정규화 층을 추가하는 것이 좋다고 조언한다. 하지만 작업에 따라 선호되는 방식이 달라 두 가지 방법 모두 확인해보는 것이 좋다.
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.BatchNormalization(),
keras.layers.Dense(300, use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("relu"),
keras.layers.Dense(100, use_bias=False),
keras.layers.BatchNormalization(),
keras.layers.Activation("relu"),
keras.layers.Dense(10, activation="softmax")
])활성화 함수 전에 배치 정규화 층을 추가하려면 은닉층에서 활성화 함수를 지정하지 않고 배치 정규화 층 뒤에 별도의 층으로 추가해야 한다. 또한 배치 정규화 층은 입력마다 이동 파라미터를 포함하기 때문에 이전 층에서 편향을 뺄 수 있다.(같은 기능을 수행하기 때문에)
BatchNormalization 클래스는 조정할 하이퍼파라미터가 적다. 보통 기본값이 잘 동작하지만 momentum 매개변수를 변경해야 할 때가 있다. 이 층이 지수 이동 평균을 업데이트할 때 이 하이퍼파라미터를 사용한다.
새로운 값 v(현재 배치에서 계산한 새로운 입력 평균 벡터나 표준편차 벡터) 가 주어지면 다음 식을 사용해 이동 평균을 업데이트한다.
중요한 다른 하이퍼파라미터는 axis 이다 이 매개변수는 정규화할 축을 결정한다. 기본값은 -1이다. 즉(배치 크기가 [샘플 개수, 특성 개수])이면 각 입력 특성이 배치에 있는 모든 샘플에 대해 계산한 평균과 표준편차를 기반으로 정규화된다. 예를 들어 이전 코드에서 첫 번째 배치 정규화 층은 784개의 입력 특성마다 독립적으로 정규화(그리고 스케일 저정과 이동)될 것이다.
만약 배치 정규화 층을 Flatten 층 이전으로 옮기면 입력 배치는 [샘플 개수, 높이, 너비] 크기의 3D가 된다. 따라서 배치 정규화 층이 28개의 평균과 28개의 표준편차를 계산한다.
그다음 동일한 평균과 표준편차를 사용하여 해당 열의 모든 픽셀을 정규화한다. 784개의 픽셀을 독립적으로 다루고 싶다면 axis=[1,2] 로 지정해야 한다.
배치 정규화 층은 훈련 도중과 훈련이 끝난 후에 수행하는 계산이 다르다. 훈련하는 동안 배치 통계를 사용하고 훈련이 끝난 후엔느 최종통계를 사용한다.
클래스 코드를 본다.
class BatchNormalizatoin(keras.layers.Layer):
...
def call(self, inputs, training=None):
...call() 메서드에서 실제 계산을 수행한다. training 매개변수가 있다. 이 매개변수의 기본값은 None이다. fit 메서드는 훈련하는 동안 이를 1로 설정한다.
만약 훈련과 테스트에 다르게 동작하는 사용자 정의 층을 만들어야 한다면 call() 메서드에 training 매개변수를 추가하고 이 매개변수를 사용해 어떤 것을 계산할지 결정한다.
BatchNormalization 은 심층 신경망에서 매우 널리 사용하는 층이되었고 보통 모든 층 뒤에 배치 정규화가 있다고 가정한다.
이 가정은 바뀔 수 있다. 최근 새로운 Fixup 가중치 초기화 기법을 사용해 매우 깊은 심층 신경망을 훈련해 복잡한 이미지 분류 작업에서 최고의 성능을 달성했다.
11.1.4 그레이디언트 클리핑
일정 임곗값을 넘어서지 못하게 잘라내는 것 순환 신경망은 배치 정규화를 적용하기 어려워 이 방법을 많이 사용한다. 다른 종류의 네트워크는 배치 정규화면 충분하다.
케라스에서 구현 시 옵티마이저를 만들 때 clipvalue와 clipnorm 매개변수를 지정한다.
optimizer = keras.optimizers.SGD(clipvalue=1.0)
model.compile(loss="mse", optimizer=optimizer)이 옵티마이저는 그레이디언트 벡터의 모든 원소를 -1.0 과 1.0 사이로 클리핑한다. 즉 훈련되는 각 파라미터에 대한 손실의 모든 편미분 값을 -1.0 에서 1.0 으로 잘라낸다. 임곗값은 하이퍼파라미터로 튜닝할 수 있다. 이 기능은 그레이디언트 벡터의 방향을 바꿀 수 있다.
예를 들어 원래 그레이디언트 벡터가 [0.9, 100.0] 라면 대부분 두 번째 축 방향으로 향한다. 하지만 값을 기준으로 이를 클리핑을 하면 [0.9, 1.0]이 되고 거의 두 축 사이 대각선 방향을 향한다. 만약 그레이디언트 클리핑이 그레이디언트 벡터의 방향을 바꾸지 못하게 하려면 clipvalue 대신에 clipnorm 을 지정하여 노름으로 클리핑해야 한다. 만약 l2 노름이 지정한 임곗값보다 크면 전체 그레이디언트를 클리핑한다.
clipnorm=1.0 으로 지정한다면 [0.008999964, 0.9999595] 로 클리핑되므로 방향을 그대로 유지되지만, 첫 번째 원소는 거의 무시된다.
훈련하는 동안 그레이디언트가 폭주한다면 임곗값으로 값과 노름을 모두 사용하여 클리핑할 수 있다.
11.2 사전훈련된 층 재사용하기
일반적으로 아주 큰 규모의 DNN을 처음부터 새로 훈련하는 것은 좋지 않다. 해결하려는 것과 비슷한 유형의 문제를 처리한 신경망이 이미 있는지 찾아본 다음 그 신경망의 하위층을 재사용하는 것이 좋다. 이를 전이 학습 transfer learning 이라고 한다.
보통 원본 모델의 출력층을 바꾼다. 비슷하게 원본 모델의 상위 은닉층은 하위 은닉층보다 덜 유용, 재사용할 층 개수를 잘 선정하는 것이 필요.
먼저 재사용하는 층을 모두 동결한다. 그다음 모델을 훈련하고 성능을 평가한다. 맨 위에 있는 한두개의 은닉층의 동결을 해제하고 역전파를 통해 가중치를 조정하여 성능이 향상되는지 확인한다. 훈련 데이터가 많을수록 많은 층의 동결을 해제할 수 있다. 이 때는 학습률을 줄이는 것이 좋다.
만약 좋은 성능을 낼 수 없고 훈련 데이터가 적다면 상위 은닉층을 제거하고 남은 은닉층을 다시 동결, 이런 식으로 재사용할 은닉층의 적절한 개수를 찾을 때까지 반복한다.
11.2.1 케라스를 사용한 전이학습
8개의 클래스만 담겨 있는 패션 MNIST 데이터셋이 있다. 누군가 이 데이터의 클래스를 분류하는 작업 A를 해결하는 모델을 만들고 꽤 좋은 성능을 얻었다. 이 모델을 ‘모델 A’라고 부른다. 샌들과 셔츠 이미지를 구분하는 작업 B를 해결하기 위해 이진 분류기를 훈련하려 한다. 레이블된 이미지 데이터는 매우 적다. 이를 위해서 모델 A와 구조가 거의 비슷한 ‘모델 B’라는 새 모델을 만들었다. 작업 B는 모델 A와 비슷하면 전이 학습을 적용
먼저 모델 A를 로드하고 이 모델의 층을 기반으로 새로운 모델을 만든다.
model_A = keras.models.load_model("my_model_A.h5")
model_B_on_A = keras.models.Sequential(model_A.layers[:-1])
model_B_on_A.add(keras.layers.Dense(1, activation="sigmoid"))출력층만 제외하고 모든 층을 재사용했다.
두 모델은 일부 층을 공유한다. 때문에 서로 영향을 받지 않기 위해 clone 하여 사용한다.
model_A_clone = keras.models.clone_model(model_A)
model_A_clone.set_weights(model_A.get_weights())이제 작업 B를 위해 B를 훈련할 수 있다. 하지만 새로운 출력층이 랜덤하게 초기화되어 있으므로 큰 오차를 만들 것임, 따라서 큰 오차 그레이디언트가 재사용된 가중치를 망칠 수 있다.
이를 피하기 위해 처음 몇 번의 에포크 동안 재사용된 층을 동결하고 새로운 층에게 적절한 가중치를 학습할 시간을 준다. 이를 위해 모든 층의 trainable 속성을 False로 지정하고 모델을 컴파일한다.
for layer in model_B_on_A.layers[:-1]:
layer.trainable = False
model_B_on_A.compile(loss="binary_crossentropy", optimizer="sgd", metrics=['accuary'])층을 동결하거나 동결을 해제한 후 반드시 모델을 컴파일해야 한다.
몇 번의 에포크 동안 모델을 훈련 후 재사용된 층의 동결을 해제한 후 훈련을 계속한다. 일반적으로 재사용된 층의 동결을 해제한 후에 학습률을 낮추는 것이 좋다. 이렇게 하면 재사용된 가중치가 망가지는 것을 막아준다.
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=4, vaildation_data=(X_valid_B, y_valid_B))
for layer in model_B_on_A.layers[:-1]:
layer.trainable =True
optimizer = keras.optimizers.SGD(lr=1e-4)
model_B_on_A.compile(loss="binary_crossentropy", optimizer = optimizer, metrics=["accuracy"])
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=16, vaildation_data=(X_valid_B, y_valid_B))전이 학습은 작은 완전 연결 네트워크에서는 잘 동작하지 않는다. 작은 네트워크는 패턴 수를 적게 학습하고 완전 연결 네트워크는 특정 패턴을 학습하기 때문, 이런 패턴은 다른 작업에 유용하지 않다. 전이 학습은 조금 더 일반적인 특성을 감지하는 경향이 있는 심층 합성곱 신경망에서 잘 동작한다.
11.2.2 비지도 사전 훈련
레이블된 훈련 데이터가 많이 않은 문제, 비슷한 작업에 대해 훈련된 모델을 찾을 수 없을 경우 비지도 사전훈련 unsupervised pretrainging 을 수행할 수 있다. 레이블이 없는 훈련 샘플을 모으는 것은 비용이 적게 들지만 여기에 레이블을 부여하는 것이 비싸다.
레이블 되지 않은 훈련 데이터를 많이 모을 수 있다면 이를 사용하여 오토인코더나 생성적 적대 신경망과 같은 비지도 학습 모델을 훈련할 수 있다. 그 다음 오토인코더나 GAN 판별자의 하위층을 재사용하고 그 위에 새로운 작업에 맞는 출력층을 추가할 수도 있다. 그다음 지도 학습으로 최종 네트워크를 세밀하게 튜닝한다.
오늘날에는 일반적으로 한 번에 전체 비지도 학습 모델을 훈련하고 오토인코더나 GAN을 사용한다.

비지도 훈련에서는 비지도 학습 기법으로 레이블이 없는 데이터로 모델을 훈련한다. 그다음 지도 학습 기법을 사용하여 레이블된 데이터에서 최종 학습을 위해 세밀하게 튜닝한다. 비지도 학습은 한 번에 하나의 층씩 훈련하거나 바로 전체 모델을 훈련할 수도 있다.
11.2.3 보조 작업에서 사전훈련
레이블된 훈련 데이터가 많지 않다면 마지막 선택 사항은 레이블된 훈련 데이터를 쉽게 얻거나 생성할 수 있는 보조 작업에서 첫 번째 신경망을 훈련하는 것이다. 그리고 이 신경망의 하위 층을 실제 작업을 위해 재사용한다.
예를 들어 얼굴을 인식하는 시스템을 만들 때 개인별 이미지가 얼마 없다면 좋은 분류기를 훈련하기에 충분하지 않다. 그러나 무작위로 많은 인물의 이미지를 수집해서 두 개의 다른 이미지가 같은 사람의 것인지 감지하는 첫 번째 신경망을 훈련할 수 있다. 이런 신경망의 하위층을 재사용해 적은 양의 훈련 데이터에서 얼굴을 잘 구분하는 분류기를 훈련할 수 있다.
자연어 처리 Natural Language Processing NLP, 텍스트 문서로 이뤄진 코퍼스를 다운로드하고 이 데이터에서 레이블된 데이터를 자동으로 생성할 수 있다. 예를 들면 일부 단어를 랜덤하게 지우고 누락된 단어를 예측하는 모델을 훈련할 수 있다. 이후 실제 작업에 이 모델을 재사용하고 레이블된 데이터를 사용해 세부 튜닝을 할 수 있다.
자기 지도 학습 self-supervised learning 은 데이터에서 스스로 레이블을 생성하고 지도 학습 기법으로 레이블된 데이터셋에서 모델을 훈련하는 방법이다.
11.3 고속 옵티마이저
아주 큰 심층 신경망의 훈련 속도는 심각하게 느릴 수 있다. 훈련 속도를 높이는 네 가지 방법으로
- 연결 가중치에 좋은 초기화 전략 사용하기
- 좋은 활성화 함수 사용하기
- 배치 정규화 사용하기
- 사전훈련된 네트워크 일부 재사용하기
또 다른 방법으로 더 빠른 옵티마이저를 사용할 수 있다.
모멘텀 최적화, 네스테로프 가속 경사, AdaGrad, RMSProp, Adam, Nadam 의 소개
11.3.1 모멘텀 최적화
공이 경사를 따라 굴러갈 때 처음에는 느리게 출발하지만 종단속도에 도달할 때까지는 빠르게 가속할 것이다. 이것이 모멘텀 최적화의 간단한 원리이다. 반대로 표준적인 경사 하강법은 경사면을 따라 일정한 크기의 스텝으로 조금씩 내려간다.

경사 하강법은 가중치에 대한 비용 함수의 그레이디언트에 학습률을 곱한 것을 차감하여 가중치를 갱신한다. 이 식은 이전 그레이디언트가 얼마였는지 고려하지 않는다. 국부적으로 그레이디언트가 아주 작으면 매우 느려질 것이다.
모멘텀 최적화는 이전 그레이디언트가 얼마였는지 중요하게 생각한다. 매 반복에서 현재 그레이디언트를 모멘텀 벡터 momentum vector m 에 더하고 이 값을 빼는 방식으로 가중치를 갱신한다. 다시 말해 그레이디언트를 속도가 아닌 가속으로 사용한다. 일종의 마찰저항으로 모멘텀momentum 이라는 새로운 하이퍼 파라미터가 등장한다. 이 값은 0(높은 저항) 과 1 사이로 설정된다. 일반적으로 0.9이다.

배치 정규화를 사용하지 않는 심층 신경망에서 상위층은 종종 스케일이 매우 다른 입력을 받게 된다. 모멘텀 최적화를 사용하면 이런 경우 큰 도움이 된다. 또한 지역 최적점을 건너뛰도록 하는 데도 도움이 된다.
케라스에서의 모멘텀 최적화 구현
optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9)단점으론 튜닝할 하이퍼파라미터가 하나 더 늘어난다는 점이지만, 모멘텀은 보통 0.9에서 잘 작동한다.
11.3.2 네스테로프 가속 경사
네스테로프 가속 경사는 현재 위치가 가중치가 아니라 모멘텀의 방향으로 조금 앞선 값에서 비용 함수의 그레이디언트를 계산한다.

NAG가 최적값에 조금 더 가깝다. 이 작은 개선이 쌓어서 확연히 빨라지게 된다. 더군다나 모멘텀이 골짜기를 가로지르도록 가중치에 힘을 가할 때 ▽1은 골짜기를 더 가로지르도록 독려하는 반면 ▽2는 계곡의 아래쪽으로 잡아당기게 된다. 이는 진동을 감소시키고 수렴을 빠르게 만들어준다.
일반적으로 기본 모멘텀 최적화보다 훈련 속도가 빠르다.
optimizer= keras.optimizers.SGD(lr=0.001, momentum=0.9, nesterov=True)
11.3.3 AdaGrad
AdaGrad 알고리즘은 가장 가파른 차원을 따라 그레이디언트의 벡터의 스케일을 감소시켜 이 문제를 해결한다.

첫 번째 단계는 그레이디언트의 제곱을 벡터 s에 누적한다(원소별 곱셈). s_i는 파라미터 a_i에 대한 비용 함수의 편미분을 제곱하여 누적한다. 비용 함수가 i번째 차원을 따라 가파르다면 s_i 는 반복이 진행됨에 따라 점점 커진다.
두 번째 단계는 경사 하강법과 거의 같다. 한 가지 큰 차이는 그레이디언트 벡터를 나누어 스케일을 조정하는 점이다.(원소별 나눗셈, 0으로 나누는 것을 막기 위한 값)
요약하면 이 알고리즘은 학습률을 감소시키지만 경사가 완만한 차원보다 가파른 차원에 대해 더 빠르게 감소된다. 이를 적응적 학습률 adaptive learning 이라고 부르며 전역 최적점 방향으로 곧장 가는데 더 도움이 된다. 학습률 파라미터를 덜 튜닝해도 된다는 장점이 있다.
AdaGrad는 너무 일찍 멈추는 경우가 종종 있어서 잘 사용하지 않는다
11.3.4 RMSProp
AdaGrad는 너무 빨리 느려져 전역 최적점에 수렴하지 못하는 위험이 있다. RMSProp는 가장 최근 반복에서 비롯된 그레이디언트만 누적함으로써 이 문제를 해결했다. 이렇게 하기 위해 지수 감소를 사용한다.
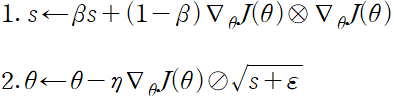
감쇠율은 0.9로 설정한다. 하이퍼파라미터가 새로 생겼지만 기본값이 잘 작동하는 경우가 많다.
optimizer = keras.optimizers.RMSprop(lr=0.001, rho=0.9)rho 매개변수가 감쇠율에 해당한다. 이 옵티마이저가 언제나 AdaGrad 보다 훨씬 더 성능이 좋다.
11.3.5 Adam과 Nadam 최적화
적응적 모멘트 추정 adaptive moment estimation 을 의미하는 Adam은 모멘텀 최적화와 RMSProp의 아이디어를 합친 것이다. 모멘텀 최적화처럼 지난 그레이디언트의 지수 감소 평균을 따르고 RMSProp 처럼 지난 그레이디언트 제곱의 지수 감소된 평균을 따른다.
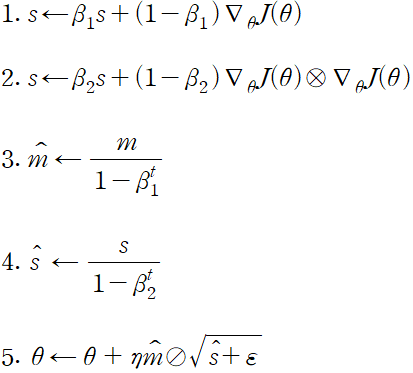
optimizer = kears.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999)Adam이 적응적 학습률 알고리즘이기 때문에 학습률 하이퍼파라미터를 튜닝할 필요가 적다. 경사 하강법보다 Adam이 사용하기 더 쉽다.
AdaMax
단계 2에서 Adam 은 s에 그레이디언트의 제곱을 누적한다. 단계 5에서 Adam은 s의 제곱근으로 파라미터 업데이트의 스케일을 낮춘다. 요약하면 Adam은 시간에 따라 감쇠된 그레이디언트의 l2 노름으로 파라미터 업데이트의 스케일을 낮춘다.
일반적으로 Adam의 성능이 더 안정적이지만 Adam 이 잘 동작하지 않는다면 시도할 수 있는 옵티마이저 중 하나
Nadam
Adam 옵티마이저에 네스테로프 기법을 더한 것, 종종 더 빠르게 수렴한다.
지금까지 논의한 모든 최적화 기법은 1차 편미분(야코비안)에만 의존한다. 최적화 이론에는 2차 편미분(헤시안. 야코비안의 편미분)을 기반으로 한 뛰어난 알고리즘이 있지만, 심층 신경망에 적용하기 매우 어렵다. 하나의 출력마다 n^2개의 2차 편미분을 계산해야 하기 때문이다.
| 희소 모델 훈련 모든 최적화 알고리즘은 대부분의 파라미터라 0이 아닌 밀집 모델을 만든다. 빠르게 실행할 모델이 필요하거나 메모리를 적게 차지하는 모델이 필요하면 희소 모델을 만들 수 있다. 간단한 방법은 모델을 훈련하고 작은 값의 가중치를 제거하는 것이다. 더 좋은 방법은 훈련하는 동안 l1 규제를 강하게 적용하는 것이다. 옵티마이저가 가능한 한 많은 가중치를 0으로 만들도록 강제한다. |
11.3.6 학습률 스케줄링
매우 작은 값에서 매우 큰 값까지 지수적으로 학습률을 증가시키면서 모델 훈련을 수백 번 반복하여 좋은 학습률을 찾을 수 있다. 그다음 학습 곡선을 살펴보고 다시 상승하는 곡선보다 조금 더 작은 학습률을 선택, 다시 초기화하고 이 학습률로 훈련한다.
일정한 학습률보다 더 나은 방법이 존재, 큰 학습률로 시작하고 학습 속도가 느려질 때 학습률을 낮추면 최적의 고정 학습률보다 좋은 솔루션을 더 빨리 발견할 수 있다 이런 전략을 학습 스케줄이라고 한다.
- 거듭제곱 기반 스케줄링 power scheduling
- 지수 기반 스케줄링 sxponential scheduling
- 구간별 고정 스케줄링 piecewise constant scheduling
- 성능 기반 스케줄링 perfomance scheduilng
- 1 사이클 스케줄링 1cycle scheduilng
성능 기반 스케줄링과 지수 기반 스케줄링 중 튜닝이 쉽고 최적점에 조금 더 빨리 수렴하는 지수 기반 스케줄링이 선호된다고 결론을 내었다. 그렇지만 1사이클 방식이 조금 더 좋은 성능을 낸다.
케라스를 통한 거듭제곱 기반 스케줄링, decay 매개변수를 지정한다.
optimizer = keras.optimizsers.SGD(lr=0.01, decay=1e-4)decay는 학습률을 나누기 위해 수행할 스텝 수의 역수이다. 케라스는 c를 1로 가정한다.
지수 기반 스케줄링과 구간변 스케줄링도 간단하다. 먼저 현재 에포크를 받아 학습률을 반환한느 함수를 정의해야 한다.
def exponential_decay_fn(epoch):
return 0.01 * 0.1 ** (epoch / 20)def exponential_decay(lr0, s):
def exponential_dacay_fn(epoch):
return lr0 * 0.1**(epoch / s)
return exponential_decay_fn
exponential_decay_fn = exponential_decay(lr0=0.01, s=20)그 다음 이 스케줄링 함수를 전달하여 LearningRateScheduler 콜백을 만들고 이 콜백을 fit 메서드에 전달한다.
lr_scheduler = keras.callbacks.LearningRateScheduler(exponential_decay_fn)
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid),
callbacks=[lr_scheduler])LearningRateScheduler 는 에포크를 시작할 때마다 옵티마이저의 learning_rate 속성을 업데이트 한다. 만약 에포크마다 스텝이 많다면 스텝마다 학습률을 업데이트하는 것이 좋다.
스케줄 함수는 두 번째 매개변수로 현재 학습률을 받을 수 있다. 다음의 스케줄 함수는 이전 학습률에 0.1^1/20 을 곱하여 동일한 지수 감쇠 효과를 낸다.
def exponential_decay_fn(epoch, lr):
return lr * 0.1**(1 / 20)모델을 저장할 때 옵티마이저와 학습률이 함께 저장된다. 새로운 스케줄 함수를 사용할 때도 아무 문제없이 훈련된 모델을 로드하여 중지된 지점부터 훈련을 계속 진행할 수 있다.
마지막으로 tf.keras는 학습률 스케줄링을 위한 또 다른 방법을 제공한다. keras.optimizers.schedules 에 있는 스케줄 중에 하나를 사용해 학습률을 정의하고 이 학습률을 옵티마이저에 전달한다. 이렇게 하면 매 스텝마다 학습률을 업데이트한다.
s = 20 * len(X_train) // 32 # 20 에포크 동안 스텝 횟수 (배치 크기 = 32)
exp_decay = ExponentialDecay(s)
history = model.fit(X_train_scaled, y_train, epochs=n_epochs,
validation_data=(X_valid_scaled, y_valid),
callbacks=[exp_decay])모델을 저장할 때 학습률과 스케줄도 함께 저장된다.
1 사이클 방식을 사용하기 위해 매 반복마다 학습률을 조정하는 사용자 정의 콜백을 만들면 된다.
11.4 규제를 사용해 과대적합 피하기
조기 종료 외에 신경망에서 널리 사용되는 다른 규제 방법들이 있다. l1, l2 규제, 드롭 아웃, 맥스-노름 규제
11.4.1 l1과 l2 규제
선형 모델에 했던 것처럼 신경망의 연결 가중치를 제한하기 위해 l2 규제를 사용하거나 희소 모델을 만들기 위해 l1 규제를 사용할 수 있다.
다음은 케라스 층의 연결 가중치에 규제 강도 0.01을 사용하여 l2 규제를 적용하는 방법을 보여준다.
layer = keras.layers.Dense(100, activation="elu",
kernel_initializer="he_normal",
kernel_regularizer=keras.regularizers.l2(0.01))l2() 함수는 훈련하는 동안 규제 손실을 계산하기 위해 각 스텝에서 호출되는 규제 객체를 반환한다. 이 손실은 최종 손실에 합산된다.
11.4.2 드롭 아웃
매 훈련 스텝에서 각 뉴런은 임시적으로 드롭아웃될 확률 p를 가진다. 즉, 이번 훈련 스텝에는 완전히 무시되지만 다음 스텝에는 활성화될 수 있다. p를 드롭아웃 비율이라고 하고 보통 10 ~ 50% 사이를 지정한다. 순환 신경망에서는 20 ~ 30% 에 가깝고 합성곱 신경망에서는 40 ~ 50% 에 가깝다.

드롭아웃의 능력을 이해하는 또 다른 방법은 각 훈련 스텝에서 고유한 네트워크가 생성된다고 생각하는 것이다. 개개의 뉴런이 있을 수도 있을 수도 없을 수도 있기 때문에 2^N 개의 네트워크가 가능하다. (N은 드롭아웃이 가능한 뉴런 수) 이는 아주 큰 값이어서 같은 네트워크가 두 번 선택될 가능성이 사실상 거의 없다. 10,000 번의 훈련 세트를 진행하면 10,000 개의 다른 신경망을 훈련하게 된다. 이 신경망은 대부분의 가중치를 공유하고 있기 때문에 아주 독립적이지 않다. 하지만 그럼에도 모두 다르다. 결과적으로 만들어진 신경망은 이 모든 신경망을 평균한 앙상블로 볼 수 있다.
중요한 기술적인 세부사항으로 꺼지지 않은 뉴런이 훈련 때보다 두 배 많은 입력 뉴런과 연결된다.(50%) 이런 점을 보상하기 위해 훈련하고 나서 각 뉴런의 연결 가중치에 0.5를 곱할 필요가 있다. 조금 더 일반적으로 말하면 훈련이 끝난 뒤 각 입력의 연결 가중치에 보존 확률(1-p)을 곱해야 한다. 또는 훈련하는 동안 각 뉴런의 출력을 보존 확률로 나눌 수 있다.
케라스에서는 keras.layers.Dropout 층을 사용하여 드롭아웃을 구현한다. 이 층은 훈련하는 동안 일부 입력을 랜덤하게 버린다. 그 다음 남은 입력을 보존 확률로 나눈다.
model = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(300, activation="elu", kernel_initializer="he_normal"),
keras.layers.Droupout(rate=0.2),
keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal"),
keras.layers.Dropout(rate=0.2),
keras.layers.Dense(10, activation="softmax")
])모델이 과대적합 되었다면 드롭아웃 비율을 늘릴 수 있다. 과소적합되었다면 드롭아웃 비율을 낮추어야 한다. 또한 많은 최신의 신경망 구조는 마지막 은닉층 뒤에만 드롭아웃을 사용한다.
수렴을 느리게 만드는 경향이 있지만 적절하게 튜닝하면 좋은 모델을 만든다.
알파 드롭아웃은 입력의 평균과 표준편차를 유지하는 드롭아웃의 한 변종이다. SELU 활성화 함수를 기반으로 자기 정규화하는 네트워크를 규제하는데 사용할 수 있다.
11.4.3 몬테 카를로 드롭아웃
드롭아웃을 사용해야 할 몇 가지 이유의 소개
- 드롭아웃을 수학적으로 정의하여 드롭아웃 네트워크와 근사 베이즈 추론 사이에 깊은 관련성을 정립했다.
- 훈련된 드롭아웃 모델을 재훈련하거나 전혀 수정하지 않고 성능을 크게 향상시킬 수 있는 몬테 카를로 드롭아웃이라 불리는 기법을 소개, 모델의 불확실성을 더 잘 층정할 수 있고 구현도 아주 쉽다.
앞서 훈련한 드롭아웃 모델을 재훈련하지 않고 성능을 향상시키는 완전한 MC 드롭아웃의 구현
y_probas = np.stack([model(X_test_scaled, training=True)
for sample in range(100)])
y_proba = y_probas.mean(axis=0)
y_std = y_probas.std(axis=0)model(X) 는 넘파이 배열이 아니라 텐서를 반환한다는 것만 빼고는 model.predict(X) 와 비슷하고 training 매개변수를 지원한다. 이 코드 예에서 training = True 로 지정하여 Dropout 층이 활성화되기 때문에 예측이 달라진다.
np.round(y_proba[:1], 2)
>>>
array([[0. , 0. , 0. , 0. , 0. , 0.11, 0. , 0.18, 0. , 0.71]],
dtype=float32)드롭아웃으로 만든 예측을 평균하면 일반적으로 드롭아웃이 없이 예측한 하나의 결과보다 더 안정적이다.
드롭아웃을 활성화하면 모델이 더 이상 확신하지 않는다. 이는 모델이 생각하는 다른 클래스에 대해 정확히 알 수 있다. 이 확률 추정의 표준 분포를 확인해볼 수도 있다.
간단히 말해서 MC 드롭아웃은 드롭아웃 모델의 성능을 높여주고 더 정확한 불확실성 추정을 제공하는 기술이다.
11.4.4 맥스-노름 규제
신경망에서 널리 사용되는 또 다른 규제 기법은 맥스-노름 규제이다. 이 방식은 각각의 뉴런에 대해 입력의 연결 가중치 w가 ||w||_2 < r 이 되도록 제한한다. 이 값 r은 맥스-노름 하이퍼파라미터이고 l2노름을 나타낸다.
맥스-노름 규제는 전체 손실 함수에 규제 손실 항을 추가하지 않는다. 대신 매 훈련 스텝이 끝나고 ||w||_2을 계산하고, 필요하면 w의 스케일을 조정한다.
r을 줄이면 규제의 양이 증가하여 과대적합을 감소시키는 데 도움이 된다. 맥스-노름 규제는 불안정한 그레이디언트 문제를 완화하는 데 도움을 줄 수 있다.
케라스에서 맥스-노름 규제를 구현하려면 다음처럼 적절한 최댓값으로 지정한 max_norm() 이 반환한 객체로 은닉층의 kernel_constraint 매개변수를 지정한다.
keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal",
kernel_constraint=keras.constraints.max_norm(1.))매 훈련 반복이 끝난 후 모델의 fit 메서드가 층의 가중치와 함께 max_norm 이 반환한 객체를 호출하고 스케일이 조정된 가중치를 반환받는다. 이 값을 사용하여 층의 가중치를 바꾼다.
11.5 요약 및 실용적인 가이드라인
기본 DNN 설정
| 하이퍼파라미터 | 기본값 |
| 커널 초기화 | He 초기화 |
| 활성화 함수 | ELU |
| 정규화 | 얕은 신경일 경우 없음, 깊은 신경망이라면 배치 정규화 |
| 규제 | 조기 종료(필요하면 l2 규제 추가) |
| 옵티마이저 | 모멘텀 최적화(또는 RMSProp, Nadam) |
| 학습률 스케줄 | 1사이클 |
네트워크가 완전 연결 층을 쌓은 단순한 모델이면 자기 정규화를 사용할 수 있다. 이 경우 아래 표에 있는 설정을 사용
자기 정규화를 위한 DNN 설정
| 하이퍼파라미터 | 기본값 |
| 커널초기화 | 르쿤 초기화 |
| 활성화 함수 | SELU |
| 정규화 | 없음(자기 정규화) |
| 규제 | 필요하다면 알파 드롭아웃 |
| 옵티마이저 | 모멘텀 최적화 (RMSProp, Nadam) |
| 학습률 스케줄 | 1사이클 |
입력 특성을 정규화해야 한다. 비슷한 문제를 해결한 모델을 찾을 수 있다면 사전훈련된 신경망의 일부를 재사용해봐야 한다.
- 희소 모델이 필요하다면 l1 규제를 사용할 수 있다. 매우 희소한 모델이 필요하다면 텐서플로 모델 최적화 툴킷을 사용할 수 있다. 이 도구는 자기 정규화를 깨뜨리므로 기본 DNN을 사용해야한다.
- 빠른 응답을 하는 모델이 필요하면 층 개수를 주링고 배치 정규화 층을 이전 층에 합쳐야 한다. LeakyReLU나 ReLU와 같이 빠른 활성화 함수를 사용한다. 희소 모델을 만드는 것도 도움이 된다. 마지막으로 부동소수점 정밀도를 낮을 수 있다.
- 위험에 민감하고 예측 속도가 매우 중요하지 않은 애플리케이션이라면 성능을 올리고 불확실성 추정과 신뢰할 수 있는 확률 추정을 얻기 위해 MC 드롭아웃을 사용할 수 있다.
'책 > Hands-On Machine Learning' 카테고리의 다른 글
| 14. 합성곱 신경망을 사용한 컴퓨터 비전 (0) | 2022.10.09 |
|---|---|
| 12. 텐서플로를 사용한 사용자 정의 모델과 훈련 (0) | 2022.10.09 |
| 10. 케라스를 사용한 인공 신경망 소개 (1) | 2022.10.08 |
| 9. 비지도 학습 (1) | 2022.10.08 |
| 8. 차원 축소 (0) | 2022.10.07 |



