기본적인 회귀 분석에는 제약식이 포함될 수 있다.
제약식을 통해 가중치가 크게 커지는 것을 방지한다.

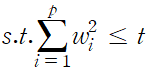
목적 함수와 제약식을 표현, 가중치 요소 제곱합이 t 보다 작다는 제약식이 추가된 형태
데이터 행렬 X는 표준화되어 평균이 0이고 분산은 1이며, y는 평균을 0으로 조정한 값이라고 가정,
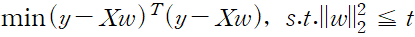
위 L2 제약식을 그림으로 표현

회색 영역이 L2 제약식, 제약식이 제곱의 형태이므로 원의 형태, 기존 추정량 w 는 외부에 있어 최종적인 추정량이 될 수 없다. L2 제약식 영역의 추정량인 w_ridge 를 구해야 한다.
최적화 문제를 라그랑주 형식으로 나타낸다.

최적의 해 계산
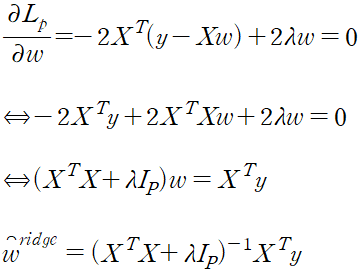
감마값에 따라 릿지 회귀 분석의 최적값이 달라진다. shrinkage parameter
- 계수의 사이즈 조절
- 정규식의 크기 조절
- 커질수록 릿지 해는 0에 가까워진다. 상수항만 남은 모델이 가까워진다.
def linear_regression_ridge(self, x, y, r):
"""
선형 회귀를 위한 정규 방정식 함수
Args:
x : 입력 데이터
y : 타깃 데이터
Return:
w : 가중치 추정량
"""
self.x_b = np.c_[x, np.ones((x.shape[0],1))] # 입력 데이터에 편향값을 위한 1의 추가
self.w = np.linalg.inv(self.x_b.T.dot(self.x_b) + r*np.identity(self.x_b.shape[1])).dot(self.x_b.T).dot(y) # 정규 방정식의 수행
return self.w2022.11.18 - [implement_ml_models] - implement_linear_regresssion
implement_linear_regresssion
선형 회귀 모형 가중치 w , 각 가중치 요소 하나하나가 우리가 구하려는 파라미터, 파라미터 값은 예측값에 영향을 미친다. 가중치는 트레이닝 데이터로부터 최소 제곱법을 사용해 구할 수 있다.
teach-meaning.tistory.com
이전의 선형 회귀의 정규 방정식에서 단위 행렬에 shrinkage parameter를 곱한 값을 추가
ne = normal_equation()
w = ne.linear_regression(train_input, test_input)
w
>>>
array([[ 36.93837597],
[-648.07755825]])
w = ne.linear_regression_ridge(train_input, test_input, 2)
w
>>>
array([[ 31.0895904 ],
[-468.21621037]])가중치가 감소된 것을 확인할 수 있다.
'implement_ml_models' 카테고리의 다른 글
| implement_momentum (0) | 2022.11.19 |
|---|---|
| implement_gradientdescent (0) | 2022.11.18 |
| implement_linear_regression (0) | 2022.11.18 |
| k-최근접 이웃 알고리즘 (0) | 2022.11.17 |
| implement_standardscaler (0) | 2022.11.17 |


