선형 판별식을 결정하는 데 최소 제곱법을 사용한 것은 모델의 예측값을 가능한 한 표적값들에 가깝게 하고자 하는 목표를 달성하기 위함이었다.
이와는 대조적으로 피셔 기준은 출력 공간상에서 클래스 간의 분리르 최대화하고자 하는 의도에서 유도되었다. 두 클래스 문제의 경우에 피셔 기준은 최소 제곱법의 특별 케이스로 볼 수 있다.
지금까지 원 핫 인코딩을 표적값에 적용하였다. 만약 다른 부호화를 적용한다면, 가중치에 대한 최소 제곱 해가 피셔 해와 동일하게 된다.
클래스 C_1 의 표적값을 N/N_1 이라고 해보자. 여기서 N_1 은 클래스 C_1 에 있는 패턴들의 숫자고, N 은 전체 패턴들의 숫자다. 이 표적값은 클래스 C_1 사전 확률의 역에 대한 근사치에 해당한다. 클래스 C_2 의 경우에는 표적값으로 -N/N_2 를 취해본다. 여기서 N_2 는 클래스 C_2 의 패턴들의 숫자다.
제곱합 오차 함수를 다음과 같이 적을 수 있다.
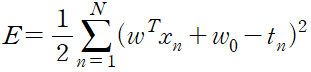
E를 w_0 와 w 에 대하여 각각 미분하고 그 값을 0으로 설정하면 다음의 식들을 얻게 된다.

위 식에서 표적값 부호화를 t_n 에 대해 적용하면 편향에 대한 다음 형태의 식을 구할 수 있다.

이 과정에서 다음의 식을 사용했다.

그리고 m 은 전체 데이터 집합의 평균으로서 다음과 같이 주어진다.

t_n 에 대해 위의 부호화를 적용하면 다음처럼 변형할 수 있다.

S_w, S_B 는 각 정의에 따른 것, 그리고 식 4 를 이용하여 편향을 대입했다. S_B w 는 항상 (m_2 - m_1) 방향을 가진다는 것을 알 수 있다. 따라서 다음과 같이 적을 수 있다.

결과적으로 피셔 기준에서 찾은 것과 가중치 벡터가 일치하게 된다. 추가적으로 편향값에 대한 공식도 찾을 수 있다. 이에 따르면 새 벡터 x 는 y(x) = w^T (x-m) > 0 일 경우에는 클래스 C_1 에, 그렇지 않은 경우에는 클래스 C_2 에 할당되어야 한다.
'개념 정리' 카테고리의 다른 글
| 판별 함수(퍼셉트론 알고리즘) (0) | 2022.12.18 |
|---|---|
| 판별 함수(다중 클래스에 대한 피셔 판별식) (1) | 2022.12.18 |
| 판별 함수(피셔의 선형 판별) (0) | 2022.12.18 |
| 판별 함수(분류를 위한 최소 제곱법) (0) | 2022.12.18 |
| 판별 함수(다중 클래스) (0) | 2022.12.18 |



