확률과 관련된 가장 중요한 계산 중 하나는 함숫값들의 가중 평균을 구하는 것이다. 확률 밀도 p(x) 하에서 어떤 함수 f(x) 의 평균값은 f(x) 의 기댓값 expectation 이라 하며, E|f| 라 적는다. 이산 분포의 경우 기댓값은 다음과 같이 주어진다.

각 x 값에 대해 해당 확률을 가중치로 사용한 가중 평균을 구하는 것이다. 연속 변수의 경우에는 해당 확률 밀도에 대해 적분을 시행해서 기댓값을 구할 수 있다.
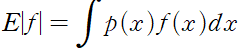
만약 유한한 N 개의 포인트를 확률 분포 또는 확률 밀도에서 추출했다면, 이산/연속 모든 경우에 각 포인트들의 유한한 합산으로 기댓값을 근사할 수 있다.

표분 추출 방법론에 대해 이 결과를 많이 활용할 것이다.
위 식의 근삿값은 lim N → INF 를 취했을 경우 정확한 값이 된다.
다변수 함수의 기댓값을 구할 경우에는 어떤 변수에 대해 평균을 내는지를 지정하여 계산할 수 있다.

위의 식은 함수 f(x,y) 의 평균값을 x 의 분포에 대해 구하라는 의미다. 위 식은 결과적으로 y 에 대한 함수가 될 것이다.
또한, 조건부 분포에 해당하는 조건부 기댓값 conditional expectation 도 생각해 볼 수 있다.

ㅇ녀속 변수에 대해서도 마찬가지로 정의를 내릴 수 있다.
f(x) 의 분산은 다음과 같이 정의된다.

분산은 f(x) 가 평균값 E(f(x)) 로부터 전반적으로 얼마나 멀리 분포되어 있는지를 나타낸다.
위 식을 전개하면 분산을 f(x) 와 f(x)^2 의 기댓값으로 표현할 수도 있다.

변수 x 그 자체의 분산도 고려해 볼 수 있다.

두 개의 확률 변수 x 와 y 에 대해서 공분산 covariance 는 다음과 같이 정의된다.

공분산은 x 값과 y 값이 얼마나 함께 같이 변동하는가에 대한 지표다. 만약 x 와 y 가 서로 독립일 경우 공분산값은 0으로 간다.
두 확률 변수 x 와 y 가 벡터일 경우 공분산은 행렬이 된다.

'개념 정리' 카테고리의 다른 글
| 확률론(베이지안 곡선 피팅) (0) | 2022.12.19 |
|---|---|
| 확률론(곡선 피팅) (0) | 2022.12.19 |
| 확률론(확률 밀도) (0) | 2022.12.19 |
| 4.2 확률적 생성 모델 (0) | 2022.12.18 |
| 판별 함수(퍼셉트론 알고리즘) (0) | 2022.12.18 |



