Implement_supportVectorMachine

서포트 벡터 머신은 서포트 벡터를 기준으로 클래스를 판별한다. 서포트 벡터 머신은 중심선과 경계선을 이용해 데이터를 구분한다. 

클래스를 구분하는 여러 방법 중 서포트 벡터 머신은 중심선과 경계선을 이용해 데이터를 구분한다. 그 경계선을 서포트 벡터라고 한다.

먼저 서포트 벡터 머신에서 중심선을 그리기 위해서 중심선에 수직인 벡터 w 를 구하는 것이 중요하다. 

중심 벡터 w 와 데이터 포인트 x 를 내적했을 때 내적값 c 가 되는 지점이 중심선이 되고, 이는 w^T x = c 라고 표현할 수 있다. 

내적값 c 가 되는 지점인 중심선을 기준으로 영역을 나눌 수 있다. 데이터 공간을 내적값이 c 보다 큰 영역과 c 보다 작은 영역으로 각각 나누면 중심선 윗부분과 아랫부분으로 나눌 수 있다.

데이터 (x_1, y_1), (x_2, y_2),...,(x_n, y_n) 가 존재할 때, 타깃 데이터는 -1 또는 1 에 속한다. 이때, 다음과 같은 초평면을 가정한다. 이 수식이 데이터 클래스를 구분하는 초평면이다.

이때, 각 영역을 나타내는 식을 간단히 나타내면 다음과 같다.

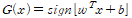
각 영역을 나타내는 식과 y_i 를 곱하면 분류식을 아래와 같이 통일할 수 있다.

경계선에 걸쳐있는 데이터는 0을 만족한다. 서포트 벡터 머신에서는 마진을 최대화하는 것이 목표이다.

중심선에 수직인 벡터 w 와 서포트 벡터에 걸쳐 있는 두 데이터 x_1, x_2 를 이용하면 마진을 구할 수 있다.

서포트 벡터 간 마진을 구하는 식

각 영역에 걸쳐 있는 벡터의 차에 중심선과 수직인 벡터를 내적하면 마진을 구할 수 있다. 위 식을 전개하면,

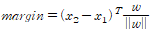
마진이 w 에 의해 결정된다는 것을 알 수 있다. (w : 중심선에 수직인 벡터)

마진을 2M 이라고 하고, 제약 조건에 마진을 최대화하는 것을 수식으로 표현,

목적 함수는 M 을 최대화하는 것이라고 표현할 수 있다. 주어진 데이터 모두가 마진 외부에 존재해야 하므로 1번째 제약 조건을 설정한다. 벡터 w 의 크기가 1이라는 제약식도 설정한다. 

위 두 조건을 합칠 수 있다. 즉, 제약식 1 에서 쓰이는 벡터 1 의 크기를 1로 만든다면 합칠 수 있을 것,

서포트 벡터 머신의 최적화 식의 표현

 

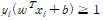
목적 함수의 제약식을 라그랑주 프리멀 함수 형태로 작성

이 식의 최적값을 구하기 위해 w, b 에 대해 미분

위 편미분 결과를 라그랑주 프리멀 함수에 대입하여 라그랑주 듀얼 함수를 구한다.

라그랑주 프리멀 함수와 듀얼 함수를 모두 만족하는 최적값임을 보이기 위해서는 KKT 조건을 만족하므로 아래 식이 성립해야 한다.

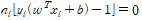
라그랑주 듀얼 함수에서 a_i >= 0 임을 알 수 있다. a_i > 0 이라면 x_i 가 서포트 벡터에 걸쳐 존재한다는 의미므로, 위 식은 0 을 만족, 1보다 크다면 경계선에 존재하지 않으므로 성립,