8.3.1 확률적 경사 하강법
심층 학습에서 자주 쓰이는 최적화 알고리즘은 SGD 와 그 변형들일 것,
자료 생성 분포로부터 독립적으로 추출한 m 개의 견본으로 이뤄진 미니배치의 평균 기울기를 취함으로써 훈련 집합 전체의 기울기의 불편 추정량을 구할 수 있다.
SGD 알고리즘의 핵심적인 매개변수는 학습 속도이다.
실제 응용에서는 시간에 따라 학습 속도를 점차 줄일 필요가 있으므로 시간에 따른 매개변수로 취급, e_k 로 k 번째 반복에서의 학습 속도를 표기,
학습 속도를 줄여야 하는 이유는 SGD 기울기 추정에 의해 ㄱ잡음이 도입되기 때문,
학습 과정에서 m 개의 훈련 견본을 무작위로 추출하는 것이 하나의 잡음 원인으로 작용하는데, 이 잡음원은 알고리즘이 최솟값에 도달해도 사라지지 안흔ㄴ다.
반면, 배치 경사 하강법에서는 총 비용함수의 기울기가 참값이 훈련이 진행되멩 따라 점점 작아져서, 최솟값에 도달하면 0이 된다.
따라서 배치 경사 하강법에는 고정된 학습 속도를 사용해도 된다.
SGD 가 반드시 수렴할 충분 조건,
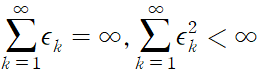

학습 속도를 시행착오를 통해서 결정할 수도 있지만, 보통의 경우는 목적함수를 시간의 함수로 간주해서 함수의ㅡ 곡선을 보고 결정하는 것이 최선이다.
주된 질문은 e_0 을 어떻게 설정할 것인가이다. 이 초기 학습 속도가 너무 높으면 비용함수가 크게 증가할 때가 많아서 학습 곡선이 요동칠 수 있다. 너무 낮을 경우 학습이 느리게 진행, 큰 비용에 머무를 위험이 있다.
일반적으로 최적의 초기 학습 속도는 처음 약 100 회 반복 이후에 최고의 성과를 내는 학습 속도 보다 높다.
따라서 알고리즘을 여러 번 반복해서 성과를 측정하고, 최고의 성과를 낸 학습 속도를 기록한 후 그보다 더 큰 값을 초기 학습 속도로 정하는 방법이 가장 바라밎ㄱ 할 때가 많다.
SGD의, 그리고 관련 미니배치 또는 온라인 기울기 기반 최적화 알고리즘이 갖추어야 할 가장 중요한 속성은, 갱신당 계산 시간이 훈련 견본의 수에 비례하지 않는 것이다. 그런 속성을 가진 알고리즘은 훈련 견본이 아주 많아도 수렴된다.
최종 시험 집합 오차가 어떤 고정된 허용치 이하가 되면 훈련 집합 전체를 다 훑지 않았어도 알고맂므을 종료하도록 설정한다면 충분히 큰 자료 집합에 대해 수렴할 수 있다.
최적화 알고리즘의 수렴 속도를 파악할 때 흔히 사용하는 측도는 J(theta) - min J(theta) 로 정의되는 초과 오차이다.
이는 현재 비용함수가 가능한 최소 비용보다 얼마나 큰지를 나타낸 값다.
SGD 를 볼록함수 문제에 적용할 때, k 회 반복 이후의 초과 오차는 O(1/r(k)) 이다. 그리고 강한 볼록 함수의 경우 O(1/k) 이다.
추가적인 조건들을 가정하지 않는 한, 이러한 한계들을 더 개선할 수는 없다.
이론적으로, 배치 경사 하강법이 확률적 경사 하강법보다 수렴 속도가 좋다. 그러나 일반화 오차는 1/k 보다 빠르게 감소할 수 없다.
그래서 이보다 더 빠르게 수렴하게 만들려고 노력할 필요는 없다고 주장하는 사람도 있다.
그보다 수렴이 빠른 것은 과대적합에 해당할 ㅜㅅ 있다.
나아가서 적은 수의 갱신 단계 이후에 확률적 경사 하강법이 가지는 여러 이득이 점근 분석에서는 잘 드러나지 않는다.
큰 자료 집합의 경우 초반에 아주 적은 수의 견본들을 평가하면서도 학습을 아주 빠르게 진행하는 SGD 의 장점이 점근적 수렴이 느리다는 단점을 능가한다.
8.3.2 momentum
확률적 경사 하강법이 인기 있는 최적화 전략이긴 하지만, 종종 학습이 느리다는 단점이 있다.
운동량 방법은 학습을 가속하기 위해 고안된 것으로, 특히 높은 곡률이나 작지만 일관된 기울기들, 잡음 섞인 기울기들이 있는 상황에서 학습을 빠르게 해준다.
운동량 알고리즘은 이전 단계 기울기들의 지수 감소하는 이동 평균을 누적해서, 그 기울기들의 방향으로 계속 이동한다.
운동량 알고리즘을 좀 더 구체적으로 살펴본다. 속도 역할을 하는 변수 v 를 사용한다. 이 속도 변수는 매개변수들이 매개변수 공간에서 움직이는 방향과 빠르기를 결정한다.
매 반복에서 알고리즘은 이 속도를 음의 기울기의 지수 감소 평균으로 설정ㅎ나다.
음의 기울기는 하나의 입자가 뉴턴의 운동 법치에 따라 매개변수 공간안에서 이동하게 만드는 힘으로 작용한다.
'심층 학습' 카테고리의 다른 글
| 8.5 학습 속도를 적절히 변경하는 알고리즘 (0) | 2023.06.10 |
|---|---|
| 8.4 매개변수 초기화 전략 (0) | 2023.06.10 |
| 8.2 신경망 최적화의 난제들 (0) | 2023.06.10 |
| 8.1.3 배치 알고리즘과 미니배치 알고리즘 (0) | 2023.06.10 |
| 8.1 학습과 순수한 최적화의 차이점 (0) | 2023.06.09 |


