실제 사례에서는 많은 종류의 입력 변수로 구성된 고차원 공간을 다뤄야 한다.
고차원 공간의 입력 변수를 다뤄야 한다는 사실은 패턴 인식 문제를 푸는 데 있어서 고려되어야 할 중요한 원소다.
단순한 접근법에의 경우 공간을 단위 크기의 칸으로 나눌 때 공간의 차원이 높아짐에 따라 필요한 칸의 개수가 기하급수적으로 늘어나는 것이다. 그만큼 많은 훈련 데이터가 필요,
다항식 곡선 피팅 문제를 다변수 입력 공간에 적용, D 개의 입력 변수가 있을 경우 3차 계수까지의 다항식의 일반 형태는 다음과 같다.

D 가 증가함에 따라 독립적인 계수의 숫자는 D^3 에 비례하여 증가한다.
M 차 다항식의 경우 계수의 숫자는 D^M 에 비례하여 증가,
기하학적인 직관은 고차원에서 매우 다르게 작용할 수 있다.
D 차원의 반지름 r = 1 인 구체를 고려, 반지름 r = 1 - e 에서 r = 1 사이에 존재하는 부피의 비율을 계산한다면 어떻게 될까? D 차원에서 반지름 r 을 가진 구체의 부피는 r^D 에 비례하여 증가한다.
따라서 다음과 같이 적을 수 있다.
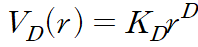
여기서 상수 K_D 는 D 에만 종속되어 있다. 따라서 다음과 같이 계산된다.

큰 D 값의 경우에는 작은 e 값에 대해서도 비율이 1에 가깝다는 것을 알 수 있다.
고차원의 공간에서는 구체 부피의 대부분이 표면 근처에 집중되어 있다는 것
고차원 공간에서의 가우시안 분포에 대해 살펴본다.
ㄷㅔ카르트 좌표에서 극좌표로 변환한 뒤에 방향성 변수들을 적분시켜 없애면 원점에서부터 반지름 r 에 대한 함수 p(r) 로 표현되는 밀도 함수를 구할 수 있다. 따라서 p(r)ar 은 반지름 r 상에 ar 의 두께에 해당하는 확률 질량을 나타나게 된다.
큰 D 값에 대해서는 가우시안 확률 질량이 껍질에 집중되어 있음,
고차원에서 발생할 수 있는 문제를 차원의 저주라고 지칭하기도 한다. 저차원 공간에서 발전시킨 아이디어들이 고차원에서 반드시 적용되지는 않는다는 점을 염두,
차원의 저주는 패턴 인식을 고차원 입력값에 적용하는 데 있어서의 중요한 문제점을 시사한다. 하지만 그렇다고 해서 고차원 입력값에 대해 사용할 수 있는 효과적인 패턴 인식 테크닉을 찾아내는 것이 불가능한 일은 아니다.
그 이유는,
실제 세계의 고차원 데이터들의 경우에 유의미한 차원의 수는 제한적,
실제 세계의 데이터는 보톡 연속적인 특성을 가지고 있다. 따라서 입력값의 작은 변화는 표적값에서도 작은 변화로만 이어지므로 지역 보간법 등의 테크닉으로 타깃 변수 예측이 가능해진다.
'패턴인식과 머신러닝' 카테고리의 다른 글
| 1.5.1 오분류 비율의 최소화 (0) | 2023.06.23 |
|---|---|
| 1.5 결정 이론 (0) | 2023.06.22 |
| 1.3 모델 선택 (0) | 2023.06.22 |
| 1.2.6 베이지안 곡선 피팅 (0) | 2023.06.22 |
| 1.2.5 곡선 피팅 - 사후 분포 최대화와 제곱합 오차 함수의 동일함 (0) | 2023.06.22 |

