2.7 고윳값 분해
수학적 대상 중에는 그것을 구성요소들로 분해해서, 표현 방식과는 무관하게 보편적인 어떤 성질을 찾아내면 더 잘 이해할 수 있는 것이 많다.
정수는 소인수 prime factor 들로 분해할 수 있다. 정수를 소인수들로 분해하면 정수의 진정한 본성에 관한 뭔가를 알아낼 수 있는 것과 비슷하게, 행렬을 다양한 방식으로 분해해 보면 성분들의 배열 형태로 표현된 행렬에서는 미처 발견하지 못한 여러 기능적인 속성이 드러난다.
가장 널리 쓰이는 행렬 분해 방법의 하나는 고윳값 분해 eigendecomposition 라는 것이다.
고윳값 분해에서는 행렬을 일단의 고유벡터들과 고윳값들로 분해한다.
정방행렬 A 의 고유벡터 eigenvector 는 하나의 0이 아닌 벡터 v 인데, A 와 곱해도 v 의 축척, scale 만 변한다는 조건을 만족한다.
Av = lambda v
스칼라 lambda 를 이 고유벡터에 대응되는 고윳값 eigenvalue 라고 부른다. 일반적으로 심층 학습에서는 우고유벡터만 다룬다.
v 가 A 의 한 고유벡터이면, 그것을 임의의 s 로 비례한 벡터 sv 도 A 의 한 고유벡터이다. 그래서 보통은 비례되지 않은 단위 고유벡터만 고려한다.
행렬 A 에 일차독립인 n 개의 고유벡터가 있으며, 이들에 대응되는 고윳값들이 있다고 하자. 이 고유벡터들을 열마다 하나씩 연결해서 행렬 V 를 만들 수 있다.
마찬가지로, 고윳값들로 하나의 벡터를 만들 수 있다. 이때, A 의 고윳값 분해 eigen decomposition 는 다음과 같이 정의된다.

고유벡터들을 열마다 연결한 고유벡터행렬, 고유값들로 만든 벡터의 대각화
이상의 논의는 특정한 고윳값들과 고유벡터들로 행렬을 구축 construction 함으로써 공간을 원하는 방향들로 확장할 수 있음을 보여준다.
그러나 이처럼 행렬을 새로 구축하는 것이 아니라 기존 행렬을 고윳값과 고유벡터들로 분해 decomposition 할 필요가 있는 경우가 많다. 행렬을 분해하면 행렬의 특정 성질을 분석하는 데 도움이 된다.
모든 행렬을 고윳값들과 고유벡터들로 분해할 수 있는 것은 아니다. 그리고 주어진 행렬의 분해가 존재하지만 실수가 아니라 복소수가 관여할 때도 있다.
실수 대칭행렬은 오직 실숫값 고유벡터들과 고윳값들로만 이뤄진 표현식으로 분해된다.
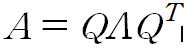
Q 는 A 의 고유벡터들로 이뤄진 직교행렬이고 LAMBDA 는 대각행렬이다. 고윳값은 Q 의 열 i 의 고유벡터와 연관되는데, 그 고유벡터를 Q_:,i 로 표기한다. Q 는 직교행렬이므로, A 는 공간을 v^(i) 방향으로 lambda_i 만큼 비례한 것이라고 할 수 있다.
임의의 실대칭행렬 A 에는 적어도 하나의 고윳값 분해가 존재한다. 그러나 그 고윳값 분해가 유일하다는 보장은 없다. 둘 이상의 고유벡터들이 동일한 고윳값을 가지고 있다면, 해당 생성공간에 놓인 임의의 직교벡터들 역시 그러한 고윳값을 가진 고유벡터들이며, 그 고유벡터들로도 동등하게 Q 를 선택할 수 있다. 관례상 LAMBDA 의 성분들을 내림차순으로 정렬해서 나열한다. 그러한 관례에서, 주어진 고윳값 분해는 오직 모든 고윳값이 유일할 때만 유일하다.
행렬의 고윳값 분해는 행렬에 관한 여러 유용한 사실을 말해 준다. 만일 고윳값 중 하나라도 0이며, 그리고 오직 그럴 때만, 행렬은 특이행렬이다. 실대칭행렬의 고윳값 분해는 f(x) = x^T A x 형태의 이차식을 ||x||_2 = 1 이라는 제약에 따라 최적화하는 데에도 활용할 수 있다. x 가 A 의 한 고유벡터와 같으면 f 는 해당 고윳값이 된다. 제약 영역 안에서 f 의 최댓값은 최대 고윳값이고 최솟값은 최소 고윳값이다.
모든 고윳갑싱 양수인 행렬을 양의 정부호 positive definite 행렬이라고 부른다. 그리고 모든 고윳값이 양수 또는 0인 행렬을 양의 준정부호 positive semidefinite 행렬이라고 부른다. 그와 비슷하게, 모든 고윳값이 음수인 행렬은 음의 정부호 negative definite 행렬, 모든 고윳갑싱 음수 또는 0인 행렬을 음의 준정부호 negative semidefinite 행렬이라고 부른다.

고유벡터와 고윳값의 효과의 예, 행렬 A 에는 두 개의 정규직교 고유벡터들이 있는데, v^(1) 의 고윳값은 lambda_1 이고, v^(2) 의 고윳값은 lambda_2 이다.
왼쪽 : 모든 단위벡터를 단위 원으로 표시한 그래프
오른쪽 : 모든 점 Au 를 표시한 그래프 A 가 공간을 v^(i) 방향으로 lambda_i 만큼 비례했기 때문에 단위 원이 그 방향으로 길쭉한 타원이 되었다.
'심층 학습 (아인 굿펠로, 오슈아 벤지오, 에런 쿠빌)' 카테고리의 다른 글
| 2. 선형대수 ( 무어-펜로즈 유사역행렬 ) (1) | 2023.10.10 |
|---|---|
| 2. 선형대수 (특잇값 분해) (0) | 2023.10.10 |
| 2. 선형대수 (특별한 종류의 행렬과 벡터) (0) | 2023.10.09 |
| 2. 선형대수 (노름) (0) | 2023.10.09 |
| 2. 선형대수 (1) | 2023.10.05 |


