2.11 행렬식
정방행렬의 행렬식 determinant 는 행렬을 실수 스칼라로 사상하는 함수로, 표기는 det(A) 이다. 행렬식은 행렬의 모든 고윳값을 곱한 것과 같다. 행렬식의 절댓값은 주어진 행렬을 곱했을 때 공간이 얼마나 확장 또는 축소되는지를 나타내는 측도라고 할 수 있다. 행렬식이 0이면 공간은 적어도 하나의 차원에서 완전히 축소되며, 결과적으로 공간의 부피가 0이 된다.
행렬식이 1이면 행렬을 곱해도 공간의 부피는 변하지 않는다.
2.12 예: 주성분 분석
기본적인 선형대수 지식만으로도 간단한 기계 학습 알고리즘의 하나인 주성분분석 principal components analysis, PCA 을 유도할 수 있다. R^n 에 있는 m 개의 점들의 집합에 유손실 압축 lossy compression 을 적용한다고 하자. 유손실 압축이란, 점들을 저장하는 데 필요한 메모리를 줄이되 정밀도 precision 을 어느 정도 잃는 것이 허용되는 압축을 말한다.
가능한 정밀도를 최소한으로 잃는 것이 바람직하다.
필요한 저장 공간을 줄이는 한 가지 방법은 이 점들을 더 낮은 차원으로 부호화하는 것이다. 각 점에 대해, 그에 대응되는 부호 벡터 code vector 를 구한다. 만일 l 이 n 보다 작다면, 그러한 원래의 자료보다 더 적은 메모리로 그러한 부호점을 저장할 수 있다.
이를 위해서는 주어진 점에 대한 부호를 산출하는 어떤 부호화 함수 encoding function, f(x) = c 와 주어진 부호로부터 원래의 점을 재구축 reconstruction 하는 복호화 함수 decoding function, x ~= g(f(x)) 가 필요하다.
PCA 를 복호화 함수로 사용할 수 있다. 구체적으로는, 복호기 decoder 를 아주 단순하게 만들기 위해 행렬 곱셈을 이용해서 부호를 다시 R^n 의 점으로 복원한다. g(c) = Dc 라고 하자. 여기서 D 는 복호화 과정을 정의하는 행렬이다.
이 복호기를 위한 최적의 부호를 계산하는 것이 어려운 문제일 수 있다. 부호화 문제를 단순하게 유지하기 위해, PCA 는 D 의 열들이 반드시 서로 직교라는 제약을 둔다.
지금까지의 문제에는 해가 여러 개 존재할 수 있다. 모든 점에 비례해서 c_i 를 감소함으로써 D_:,i 의 비례 정도를 증가할 수 있기 때문이다. 이 문제의 해가 고유함을 보장하기 위해, D 의 열들이 모두 단위 노름이어야 한다는 제약을 도입한다. 이러한 기본 착안을 구현 가능한 알고리즘으로 만들려면, 우선 각 입력점 x 에 대한 쵲거의 부호점 c* 를 생성하는 방법을 고안해야 한다.
한 가지 방법은 입력점 x 와 그것의 재구축 결과인 g(c*) 사이의 거리를 최소화하는 것이다. 이 거리는 노름으로 측정할 수 있다.
주성분 분석 알고리즘에서는 L^2 노름을 사용한다.

L^2 노름 대신 제곱 L^2 노름을 사용해도 된다. L^2 노름은 음이 아닌 수이고, 제곱 연산은 음이 아닌 인수에 대해 단조 증가하므로, 결과적으로 두 노름 모두 같은 c 값에 의해 최소화된다.
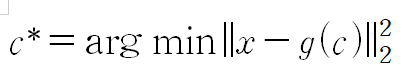
최소화 대상 함수를 따로 전개, 정리해본다.



그런데 최소화 대상 함수에서 첫 항은 c 에 의존하지 않으므로 생략해도 된다.

더 나아가서, 이 공식에 g(c) 의 정의를 대입해서 정리하면 다음이 나온다.


이제 벡터 미적분 vector calculus 를 이용해서 이 최적화 문제를 풀 수 있다.

공식을 이렇게 만들면 알고리즘의 효율성이 좋아진다. x 를 그냥 행렬 벡터 곱셈 연산 한 번만 사용해서 최적으로 부호화할 수 있다.
벡터를 부호화할 때는 다음과 같은 부호화 함수를 적용한다.

그리고 행렬 곱셈을 하나만 더 사용하면 PCA 재구축 연산을 정의할 수 있다.

다음으로, 부호화 행렬 encoding matrix, D 를 선택해야 한다. 이를 위해, 입려고가 재구축 사이의 L^2 거리를 최소화한다는 착안을 고찰해본다. 모든 점을 동일한 행렬 D 로 복호화할 것이므로 점들을 따로 고려할 필요가 없다. 대신, 모든 차원과 모든 점에 관해 계산한 오차들로 이루어진 행렬의 프로베니우스 노름을 최소화해야 한다.

이제 이러한 D* 를 구하는 알고리즘을 유도해 보자. 우선 l=1 인 경우를 고찰한다. 이 경우 D 는 그냥 하나의 벡터 d 이다.
D 를 d 로 표현하면 문제는 다음으로 정리된다.

이 공식은 대입을 아주 직접 적용해서 얻은 것이라서 유도 과정이 간단하지만, 공식의 스타일이 아름답지는 않다.
이 공식에서는 스칼라 d^T x^(i) 가 벡터 d 의 오른쪽에 있다. 그러나 일반적으로는 스칼라 계수를 그 적용 대상인 벡터의 왼쪽에 두는 것이 관례이다. 그러한 관례에 따라, 위 식을 다시 표현한다.

또는, 스칼라의 전치가 스칼라 자신이라는 점을 이용해서 다음과 같이 좀 더 정리할 수도 있다.

지금 단계에서는 문제를 개별 견본 벡터들에 관한 합으로 표현하는 대신, 견본들로 이루어진 하나의 단일한 설계 행렬 design matrix 로 표현하는 것이 도움이 될 수 있다. X 이 점들을 서술하는 모든 벡터를 쌓아서 정의한 행렬이라고 하자. 즉, X_i,:=x^(i)T 이다. 그러면 문제를 이전과는 다른 형태로 표현할 수 있다.

프로베니우스 노름 부분을 단순화할 수 있다.

이러한 최적화 문제를 고윳값 분해로 풀 수도 있다.
구체적으로 말하면, 최적의 d 는 X^TX 의 가장 큰 고윳값에 대응되는 고유벡터이다.
'심층 학습 (아인 굿펠로, 오슈아 벤지오, 에런 쿠빌)' 카테고리의 다른 글
| 3.2 확률변수 (1) | 2023.10.10 |
|---|---|
| 3. 확률론과 정보 이론 (0) | 2023.10.10 |
| 2. 선형대수(대각합 연산자) (0) | 2023.10.10 |
| 2. 선형대수 ( 무어-펜로즈 유사역행렬 ) (1) | 2023.10.10 |
| 2. 선형대수 (특잇값 분해) (0) | 2023.10.10 |


