1.1 예시 : 다항식 곡선 피팅

인공적인 데이터 sin(2 pi x) 함수를 활용하여 데이터 생성, 타깃 변수에는 약간의 랜덤한 노이즈를 포함시킨다.

N 개의 관찰값 x 로 이루어진 훈련 집합 x 와 그에 해당하는 표적값이 주어졌다고 해본다.

입력 데이터 집합 x 는 서로 간에 같은 거리를 가지도록 균등하게 x_n 값들을 선택하여 생성, 포적 데이터 집합의 값들은 함수 sin(2 pi x) 의 출력값에 가우시안 분포를 가지는 약간의 노이즈를 더해서 만들었다. 

 

실제 데이터 집합은 어떤 특정한 규칙성을 가지지만, 각각의 관찰값들은 보통 랜덤한 노이즈에 의해 변질되곤 한다. 이러한 노이즈는 본질적으로 확률적인 과정을 통해 발생할 수 있는데, 관찰되지 않은 변수의 가변성에서 기인한다.

 

목표는 훈련 집합들을 사용해서 어떤 새로운 입력값이 주어졌을 때 타긴 변수를 예측하는 것으로,

기저에 있는 함수, sin(2 pi x) 를 찾아내는 것이 예측 과정에 암시적으로 포함된다.

이는 한정된 데이터 집합으로부터 일반화를 시행하는 과정이 필요하기 때문에 본질적으로 어려운 문제다. 

 

게다가 관측된 값들은 노이즈로 인해 변질되어 있어서 각각의 주어진 x^ 에 대해서 어떤 값이 적합한 t^ 인지가 불확실하다. 확률론은 이러한 불확실성을 정확하고 정량적으로 표현하는 데 도움을 줄 것이다. 

의사 결정 이론은 ㅇ특정 기준에 따라 최적의 예측을 하느 ㄴ데있어서 확률적인 표현을 활용할 수 있도록 해준다.

 

곡선을 피팅하는 데 있어 다음과 같은 형태의 다항식을 활용한다.

M 은 이 다항식의 차수 order 이며, 다항식의 계수를 함께 모아서 벡터 w 로 표현할 수 있다.

다항 함수 y(x, w) 는 x 에 대해서는 비선형이지만, 계수 w 에 대해서는 선형이다. 

 

다항식을 훈련 집합 데이터에 피팅해서 계수의 값들을 정할 수 있다. 훈련 집합의 표적값들의 값과 함숫값과의 오차를 측정하는 오차 함수 error function 을 정의하고 이 함수의 값을 최소화하는 방식으로 피팅할 수 있다. 

 

가장 널리 쓰이는 오차 함수 중 하나는 다음과 같다. 

이 함수의 결괏값은 양수이며, 오직 함수가 정확히 데이터 포인트들을 지날 때만 값이 0이 된다는 사실을 명심해 두면 된다.

 

E(w) 를 최소화하는 w 값을 선택함으로써 이 곡선 피팅 문제를 해결할 수 있다. 오차 함수가 이차 다항식의 형태를 지니고 있기 때문에 이 함수를 계수에 대해 미분하면 w 에 대해 선형인 식이 나올 것이다. 

따라서 이 오차 함수를 최소화하는 w 는 유일한 값인 w* 을 찾아낼 수 있다. 

 

다항식의 차수 M 을 결정하는 문제가 여전히 남아 있다. 이 문제가 바로 모델 비교 model comparison 혹은 모델 결정 model selection 이라 불리는 예시에 해당한다.

 

차수가 너무 높아 심하게 진동하는 과적합 over fitting 의 예

 

M=9 인 다항식 집합은 M = 3 인 다항식 집합이 만들어낼 수 있는 결괏값을 전부 만들어 내는 것이 가능하다. 

피팅의 성능은 M 이 증가함에 단조 증가해야 한다고 결론을 내릴 수도 있다. 

 

사용되는 데이터 집합의 크기가 달라지는 경우, 모델의 복잡도가 일정할 때 데이터 집합의 수가 늘어날수록 괒거합 문제가 완화되는 것을 ㅗ학인할 수 있다. 

즉, 데이터 집합의 수가 클수록 더 복잡한 모델을 활용하여 피팅할 수 있다는 의미, 

 

과적합 문제를 해결하기 위해 자주 사용되는 기법 중 하나는 정규화 regularization 이다. 오차 함수에 계수의 크기가 커지는 것을 막기 위한 페널티항을 추가하는 것이다. 

가장 단순한 형태로 각각의 계수들을 제곱하여 합하는 것이다.

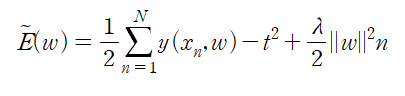
계수 lambda 가 정규화항의 제곱합 오류항에 대한 상대적인 중요도를 결정짓는다. 

위 식의 오차 함수의 최솟값을 찾는 문제 역시 닫힌 형식이기 때문에 미분을 통해서 유일해를 찾아낼 수 있다. 이 방법을 수축법 shrinkage method 라고 한다. 방법 자체가 계수의 크기를 수축시키는 방식을 이용하기 때문,

 

지금까지의 결과를 바탕으로 모델 복잡도를 선택하는 방법 하나를 생각해 볼 수 있다. 그것은 데이터 집합을 훈련 집합 test set 과 검증 집합 validation set 으로 나누는 것이다.

훈련 집합은 계수 w 를 결정하는 데 활용하고 검증 집합은 모델 복잡도를 최적화하는 데 활용하는 방식이다.