초평면의 성질 두 가지
- 최근접 재구성 성질 : 샘플 포인트와 초평면의 거리가 충분히 가까워야 함
- 최대 기분 성질 : 샘플 포인트가 초평면상의 투영과 분리 가능해야 함
먼저, 모든 데이터 샘플을 0 중심으로 처리했다고 가정

그리고 투영 변환 후 새로운 좌표계 w 는 정규직교 벡터라고 가정한다.
만약 새로운 좌표계 중에서 부분좌표를 잃었다면 차원은 줄어들며, 샘플 x는 저차원 좌표계상의 z 로 투영되고, z = wx 은 저차원 좌표계에서 x의 좌표가 된다.
만약 z를 기반으로 다시 x를 구성한다면

위를 얻는다.
모든 훈련 데이터 세트에서 원래의 샘플 x와 투영에 기반해 재구성된 샘플 사이의 거리는 아래 식이다.

const는 상수를 뜻한다.

최근접 재구성 성질에 의해 위 식은 최소화되어야 하고, w가 정규직교기저이므로

이는 공분산 행렬이다. 따라서 다음 식이 된다.

이것이 바로 주성분 분석의 최적화 목표이다.
최대 가분성 관점에서도 이를 해석할 수 있다. 투영 후 샘플들의 분산을 최대화하기 위한 식
공분산 행렬은

최적화 목표는 다음과 같이 쓸 수 있다.

위 두 식은 동일하다.
두 식에 대해 라그랑주 승수를 사용하면 다음을 얻는다.
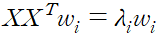
따라서 공분산 행렬 XX^T 에 대해서만 고윳값 분해를 진행하면 특잇값 배열 순서를 얻을 수 있다. 앞에서부터 d'개 특잇값에 대응하는 고윳값들로 W를 구성한다.
이것이 바로 주성분 분석의 행이다.
'개념 정리' 카테고리의 다른 글
| PCA 2 (0) | 2022.11.16 |
|---|---|
| 커널 선형 차원 축소 (0) | 2022.11.16 |
| 선형 판별분석 LDA Linear Discriminant Analysis (0) | 2022.11.16 |
| 임베딩 (0) | 2022.11.16 |
| k-최근접 이웃 (0) | 2022.11.15 |



