다층 퍼셉트론은 퍼셉트론의 층이 여러 개인 것, 함수 형태로 표현하면,

위와 같은 체인 구조가 많이 쓰인다.
오차 역전파
다층 퍼셉트론에서 최적값을 찾아가는 과정은 오차 역전파 방법을 사용
input = np.array([[1,2,3]])
target = np.array([[0.5,0.1]])(1) 가중치 초기화
임의의 가중치 지정 ( 이러한 초기 가중치를 설정하는 방법도 존재 )
w1 = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
w2 = np.array([[0.7,0.9],[0.8,0.1]])
b1 = np.array([[0.5],[0.5]])
b2 = np.array([[0.3],[0.3]])wl는 각 층 l 에 대한 가중치고 w의 각 행 값은 다음 노드의 입력에 대한 가중치,
여기에 각 층 l 에 대한 편향 bl이 추가된다.
(2) 순전파 계산 수행
입력에 가중치 연산을 수행, 이는 각 은닉층 노드의 입력이 된다. 은닉층 노드 개수 n 개의 결과 생성
g1 = w1.dot(input.T)+b1
g1
>>>
array([[2.7],
[3.3]])
각 은닉층 노드의 입력에 활성화 함수 연산, 이 경우 시그모이드 함수를 사용한다. (함수로 사용할 수 있을 것)
h1 = 1/(1+np.exp(-g1))
h1
>>>
array([[0.93702664],
[0.96442881]])출력층 노드의 입력의 연산
z1 = w2.dot(h1)+b2
z1
>>>
array([[1.82390458],
[1.1460642 ]])각 출력층 노드의 입력에 대한 시그모이드 함수 연산
y1 = 1/(1+np.exp(-z1))
y1
>>>
array([[0.86103399],
[0.75879129]])이를 통해 최종 출력층 결과를 구할 수 있다.
(3) 비용 함수 정의 및 1차 미분식 구하기

동일한 방법으로 활성화 함수의 미분값을 구한다.

미분값은 오차 역전파법을 적용하기 위함
(4) 역전파를 통한 1차 미분값 계산
출력층에서 은닉층으로 거꾸로 올라가는 과정, 수식의 표현

가중치나 편향이 변했을 때 출력값의 변화를 구하기 위해 미분,
위 식을 바탕으로 은닉층에서 출력층까지 연결되는 가중치의 변화에 따른 비용 함수의 변화량을 계산

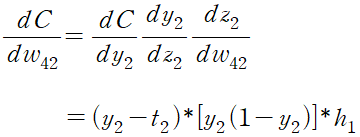

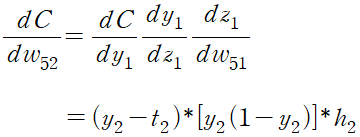
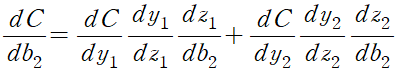
c = y1*(1-y1)*((y1.T-target).T).dot(h1.T)
c
>>>
array([[0.04047892, 0.04166268],
[0.11298352, 0.11628758]])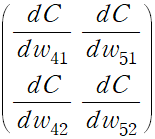
c_b = (y1*(1-y1)).T.dot((y1.T-target).T)
c_b
>>>
array([[0.16377596]])위 계산 과정을 통해 각 가중치 값의 변화에 따른 비용 함수 C 의 변화량을 구할 수 있었다.
은닉층에서 입력층으로의 계산

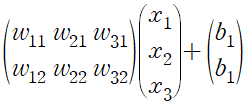
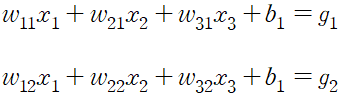
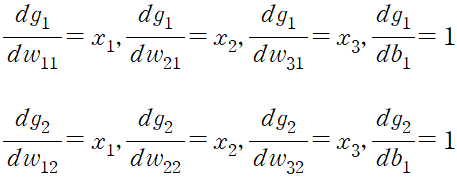

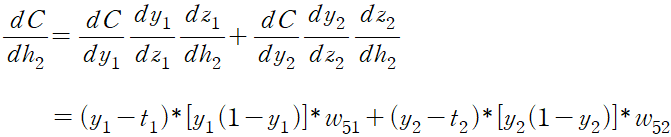
c_y = y1-target.T
c_y
>>>
array([[0.36103399],
[0.65879129]])
y_z = (y1*(1-y1))
y_z
>>>
array([[0.11965446],
[0.18302707]])
c_h = c_y.T*y_z.T@w2
c_h
>>>
array([[0.12670084, 0.05093706]])각 은닉층 노드에 대한 변화량을 얻을 수 있다.
이 후 이를 이용해 입력층의 가중치들의 변화에 따른 비용 함수의 변화량을 계산할 수 있다.
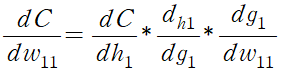

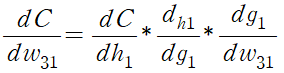


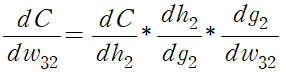
입력층의 가중치에 대한 비용 함수의 변화를 계산하기 위해, 은닉층까지의 변화율과 해당 은닉층의 활성화 함수에 대한 변화율, 은닉층의 입력과 가중치에 대한 변화율을 이용해 계산한다.
h_g = h1*(1-h1)
h_g
>>>
array([[0.05900771],
[0.03430588]])
c_w1 = (c_h*(h_g.T)).T*input
c_w1
>>>
array([[0.00747633, 0.01495265, 0.02242898],
[0.00174744, 0.00349488, 0.00524232]])나온 결과는

위 형태를 띈다.
마지막으로 편향에 대한 변화율을 계산,

c_h 은닉층의 입력까지의 연산은 가중치와 동일, 여기에 각 편향에 대한 변화율의 연산을 수행한다(1의 값)
c_b1 = c_h.dot(h_g)
c_b1
>>>
array([[0.00922377]])이렇게 얻은 모든 가중치들에 대한 오차 함수의 변화량을 통해 파라미터 업데이트를 진행한다.
'implement_ml_models' 카테고리의 다른 글
| implement_cnn (0) | 2022.11.22 |
|---|---|
| implement_activation (0) | 2022.11.21 |
| implement_perceptron (0) | 2022.11.21 |
| implement_nadam (0) | 2022.11.20 |
| implement_adaMax (0) | 2022.11.20 |



