물체의 속력이 변하고 있을 때는 순간속력을 측정하는 게 중요하다. 어느 한 순간의 이동 속력,
아주 짧은 시간 동안의 평균속력을 계산한다면 순간속력과 근사값을 계산해 낼 수 있다.
속력이 계속 변하는 물체의 순간속력을 알려면, 시간별 위치함수 곡선의 기울기를 알아야 한다.
곡선의 기울기가 일정하지 않은 이유는 속력이 일정하지 않기 때문, 곡선의 기울기를 직접 알아낼 수는 없지만, 만약 곡선의 한 점에서 그 점에서의 곡선의 기울기와 동일한 기울기를 가진 직선을 그린다면 가능하다.
두 점의 좌표는 (a, f(a)), (a+△a,f(a+△a))이다.
두 점을 잇는 직선의 기울기 = f(a+△a) - f(a) / a+△a - a
이런 종류의 직선을 할선이라고 한다. 곡선과 두 개의 점에서 교차하는 직선,
한 개의 점에서만 교차할 때는 접선이라고 부른다.
할선을 접선에 가깝게 움직이면 △a 를 점점 더 작게 만들어서 두 점이 가까워지도록 할 수 있다.

f(x)가 x^2 일 때,
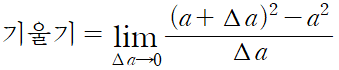

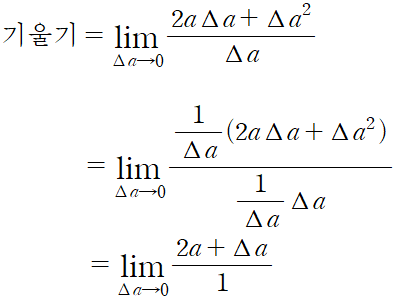
△a 가 0 에 가까워질수록 2a+△a 는 2a 에 가까워진다.
'미적분' 카테고리의 다른 글
| 6. 최적값과 상대율 (0) | 2022.12.21 |
|---|---|
| 5. 삼각함수의 도함수 (0) | 2022.12.21 |
| 4. 복잡한 함수의 도함수 (2) | 2022.12.21 |
| 도함수를 이용하여 그래프 그리기 (0) | 2022.12.20 |
| 2. 도함수 구하기 (0) | 2022.12.20 |



