가장 중요한 연속 확률 분포, 정규 분포 normal distribution, 가우시안 분포 Gaussian distribution
단일 실수 변수 x 에 대한 가우시안 분포
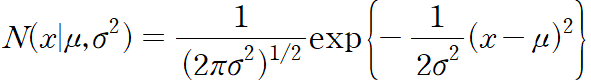
mu 는 평균 mean, sigma^2 은 분산 variance 이다. sigma는 표준 편차 standard deviation, 분산의 역수에 해당하는 값, beta 정밀도, precision
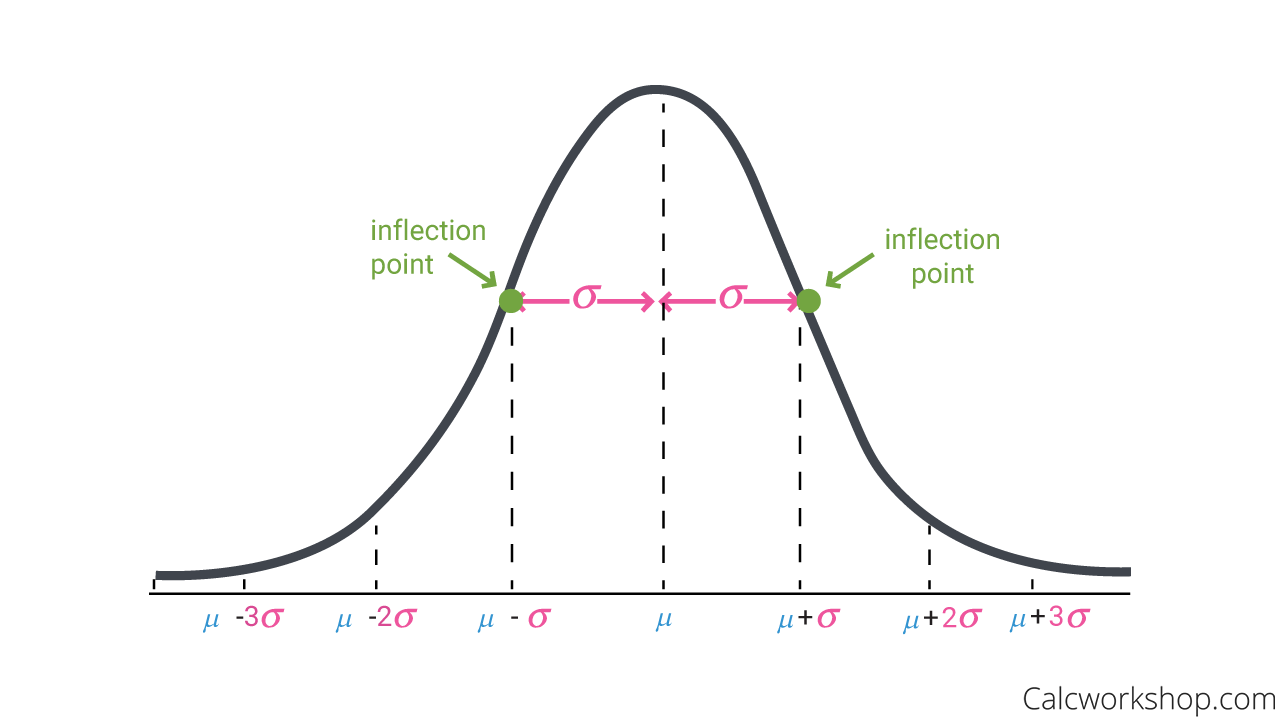

분포의 성질과 정규화의 확인 가능,
가우시안 분포를 따르는 임의의 x 에 대한 함수의 기댓값을 구할 수 있다. 특히, x 의 평균값은 다음과 같다.
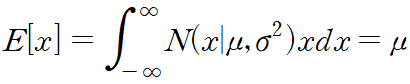
평균값 매개변수 mu 가 x 의 기댓값과 동일함을 확인할 수 있다. 이와 비슷하게 x 에 대한 이차 모멘트 계산,
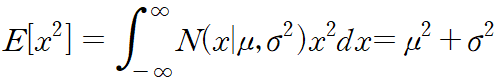
위 두 식으로부터 분산을 다음과 같이 계산할 수 있다.

sigma^2 이 분산임을 확인할 수 있다.
연속 변수로 이루어진 D 차원 벡터 x 에 대한 가우시안 분포
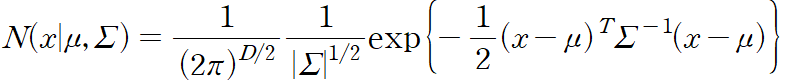
D 차원 벡터 mu 는 평균값, D*D 행렬 SIGMA 는 공분산, |SIGMA| 는 SIGMA 의 행렬식이다.
관측된 데이터 x 를 살펴본다. 이는 관측된 N 개의 스칼라 변수 x 를 지칭한다.
평균값 mu 와 분산 sigma^2 를 가지는 가우시안 분포에서 관측값들을 독립적으로 추출했다고 가정, 데이터 집합으로부터 이 매개변수들을 결정하는 것이 목표이다.
같은 분포에서 독립적으로 추출된 데이터 포인트들을 독립적이고 동일하게 분포 independent and identically distributed 되었다고 한다.
두 독립 사건의 결합 확률은 각 사건의 주변 확률의 곱이라는 것을 살펴보았다. 데이터 집합 x 는 i.i.d 이기 때문에 mu 와 sigma^2 가 주어졌을 때의 조건부 확률은 다음과 같이 적을 수 있다.
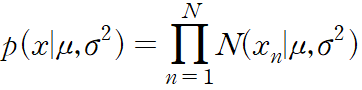
mu 와 sigma^2 의 함수로 보면 이 식의 가우시안 분포의 가능도 함수에 해당한다.
관측된 데이터 집합을 바탕으로 확률 분포의 매개변수를 결정하는 표준적인 방법 중 하나는 가능도 함수를 최대화하는 매개변수를 찾는 것이다.
매개변수를 바탕으로 데이터의 확률을 최대화하는 것
가능도 함수를 최대화하는 방식으로 알려지지 않은 가우시안 분포의 매개변수 mu 와 sigma^2 를 찾는 것을 진행,
로그 함수는 변수에 대해 단조 증가하는 함수이므로 로그를 취한 후 최댓값을 찾는 것은 원래 함수의 최댓값을 찾는 것과 동일하다.
로그 가능도 함수를 다음과 같이 적을 수 있다.
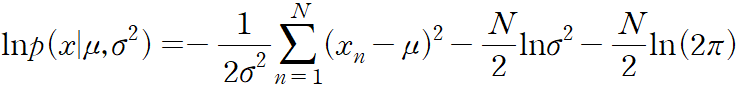
mu 에 대해 위 식의 최댓값을 찾으면 당므의 최대 가능도 해를 찾ㅇ르 수 있다.
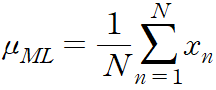
이는 바로 관찰된 값들의 평균인 표본 평균이다.
비슷한 방식으로 최댓값을 sigma^2 에 대해 찾으면 분산에 대한 최대 가능도 해를 다음과 같이 찾을 수 있다.
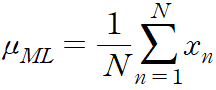
이는 표본 평균에 대해 계산된 표본 분산이다.
mu 와 sigam^2 에 대해 결합 극대화를 하려 하고 있다. 그러나 가우시안 분포의 경우에는 mu 에 대한 해가 sigma^2 에 대한 해와 연관되어 있지 않다. 따라서 계산의 순서가 상관없다.
단변량 가우시안 분포를 기준으로 하여 최대 가능도 방법을 통해 계산한 매개변수값이 어던 문제를 가지고 있는지 살펴본다. 최대 가능도 방법이 구조적으로 분포의 분산을 과소평가하게 되는 것을 확인할 수 있다.
이는 편향 bias 현상의 예시로써, 다항식 곡선 피팅에서의 과적합 문제와 연관되어 있다.
최대 가능도 해인 mu_ML 과 sigma^2_ML 은 데이터 집합 x_1, ..., x_N 의 함수다.
각 데이터 집합의 값에 대해 이들의 기댓값을 고려,
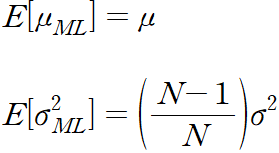
따라서 평균적으로 최대 가능도 추정은 평균은 올바르게 추정할 수 있지만 분산은 (N - 1) / N 만큼 과소평가하게 된다.
분산 추정치는 비편향임을 알 수 있다.
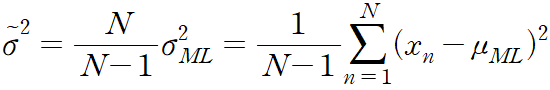
최대 가능도 방법의 편향 문제는 우리가 앞에서 살펴본 다항식 곡선 피팅에서의 과적합 문제의 근본적인 원인에 해당한다.
초초
'패턴인식과 머신러닝' 카테고리의 다른 글
| 1.2.6 베이지안 곡선 피팅 (0) | 2023.06.22 |
|---|---|
| 1.2.5 곡선 피팅 - 사후 분포 최대화와 제곱합 오차 함수의 동일함 (0) | 2023.06.22 |
| 1.2.3 베이지안 확률 - 불확실성의 정량화 (0) | 2023.06.21 |
| 1.2.2 기댓값과 공분산 (0) | 2023.06.21 |
| 1.2.1 확률 밀도 (0) | 2023.06.21 |



