가장 단순한 선형 회귀 모델은 입력 변수들의 선형 결합을 바탕으로 한 모델이다.

이 모델은 종종 선형 회귀 모델이라고 불린다.
가장 중요한 성질은 이 모델이 매개변수의 선형 함수라는 것이다.
또한, 이 모델은 입력 변수 _i 의 선형 함수이기도 한데, 이러한 성질 때문에 선형 회귀 모델에는 심각한 한계점이 존재한다.
이 한계점을 극복하기 위해서 다음처럼 입력 변수에 대한 고정 비선형 함수들의 선형 결합을 사용할 수 있다.

여기서 phi_j(x) 가 기저 함수 basis function 다.
모델의 매개변수 숫자는 M 이 된다.
매개변수 w_0 는 데이터에 있는 고정된 오프셋을 표현할 수 있게 해준다. 이를 편향 bias 매개변수라고 부르기도 한다.
편의를 위해서 추가적인 의사 기저 함수를 정의 phi_0(x) = 1, 그러면 다음과 같이 표현할 수 있다.
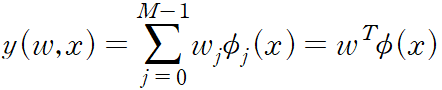
많은 패턴 인식의 응용 사례에서는 원 데이터 변수에 전처리나 특징 추출 과정을 적용하게 된다. 원래의 변수가 벡터 x 라 한다면, 특징들은 기저 함수 phi_j(x) 를 바탕으로 표현할 수 있다.
비선형 기저 함수들을 사용하여 함수 y(x,w) 가 입력 벡터 x 에 대한 비선형 함수가 되도록 할 수 있다.
다양한 다른 함수들이 기저 함수로 사용될 수 있다.

mu_j 는 입력 공간에서의 기저 함수의 위치를 결정하며, 매개변수 s 는 공간적 크기를 결정한다.
위식은 가우시안 기저 함수라고 불린다.
또 다른 기저 함수의 예는 시그모이드 기저 함수

sigma(a) 는 다음처럼 정의되는 로지스틱 시그모이드 함수

'패턴인식과 머신러닝' 카테고리의 다른 글
| 3.1.2 최소 제곱의 기하학적 의미 (0) | 2023.06.25 |
|---|---|
| 3.1.1 최대 가능도와 최소 제곱 (0) | 2023.06.24 |
| 3. 선형 회귀 모델 - 복잡한 모델들의 토대 (0) | 2023.06.24 |
| 2.1 이산 확률 변수 (0) | 2023.06.24 |
| 2. 확률 분포 (0) | 2023.06.24 |


