타깃 변수 t 는 결정 함수 y(x, w) 와 가우시안 노이즈의 합으로 주어진다고 가정,
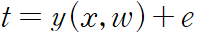
e 는 0을 평균으로, beta 를 정밀도로 가지는 가우시안 확률 변수다.
따라서 다음과 같이 적을 수 있다.
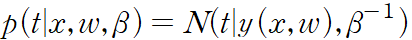
제곱 오류 함수를 가정할 경우 새 변수 x 에 대한 최적의 예측값은 타깃 변수의 조건부 평균으로 주어질 것이다. 위 형태의 가우시안 조건부 분포의 경우에 조건부 평균은 다음과 같다.

노이즈의 분포가 가우시안이라는 가정은 x 가 주어졌을 때의 t 의 조건부 분포가 단봉 형태임을 내포,
입력 데이터 집합과 그에 해당하는 타깃 변수를 고려,
타깃 변수들을 t 로 지칭한 열 벡터로 무리지을 수 있다. 이 데이터 포인트들이 분포로부터 독립적으로 추출되었다는 가정하에 다음 혀애를 가지는 가능도 함ㅁ수를 얻을 수 있다.
이 가능도 함수는 조절 가능한 매개변수 w 와 beta 의 함수다.

회귀나 분류 같은 지도 학습 문제의 경우에 입력 변수의 분포를 모델하려 하지 않는다. 따라서 x는 언제나 조건부 변수의 집합에 포함되어 있을 것이다.
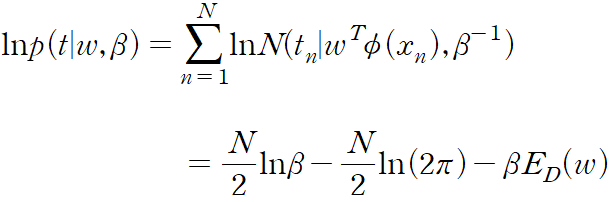
제곱합 오류 함수는 다음과 같이 정의

가능도 함수에 최대 간으도 방법을 적용하여 w 와 beta 를 구할 수 있다.
먼저 w 에 대해 극대화하는 경우를 고려,
가능도 함수를 최대화하는 것은 제곱합 오류 함수 E_D(w) 를 최소화하는 것과 동일하다.
식의 로그 가능도 함수의 기울기는 다음과 같다.

기울기를 0으로 놓으면 다음을 얻게 된다.
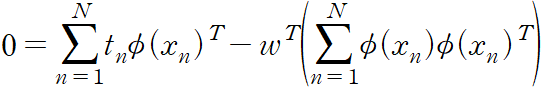
이를 w 에 대해 풀면 다음을 얻을 수 있다.
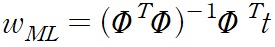
위 식을 최소 제곱 문제의 정규 방정식 normal equation 라고 부른다. PHI 는 N*M 행렬로, 설계 행렬 design matrix 라 불린다. 설계 행렬의 각 원소는 PHI_nj = phi_j(x_n) 으로 주어진다.

위 식을 PHI 의 무어-펜로즈 유사-역행렬이라고 한다.
역행렬의 개념을 정사각이 아닌 행렬들에 대해서 일반화한 것이라고 보면 된다.
행렬 PHI 가 정사각이고 가역행렬이면 (AB)^-1 = B^-1 A^-1 이라는 성질을 바탕으로 PHI^dagger ≡ PHI^-1 임을 확인할 수 있다.
편향 매개변수 w_0 의 역할에 대해 관찰,
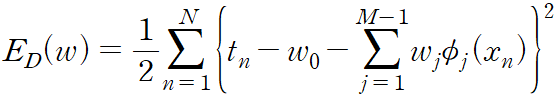
w_0 에 대한 미분값을 0으로 놓고 w_0에 대해 풀면 다음을 구할 수 있다.

여기서 다음을 정의

편향 w_0 가 훈련 집합의 타깃 변수들의 평균과 기저 함숫값 평균들의 가중 합 사이의 차이를 보상한다는 것을 알 수 있다.
로그 가능도 함수를 노이즈 정밀도 매개변수 beta 에 대해 최대화하면 다음을 얻게 된다.

노이즈 정밀도의 역이 회귀 함수 근처 타깃 변수들의 잔차 분산으로 주어진다는 것을 알 수 있다.
'패턴인식과 머신러닝' 카테고리의 다른 글
| 3.1.3 순차적 학습 (0) | 2023.06.25 |
|---|---|
| 3.1.2 최소 제곱의 기하학적 의미 (0) | 2023.06.25 |
| 3.1 선형 기저 함수 모델 (0) | 2023.06.24 |
| 3. 선형 회귀 모델 - 복잡한 모델들의 토대 (0) | 2023.06.24 |
| 2.1 이산 확률 변수 (0) | 2023.06.24 |


