최대 가능도 해와 같은 일괄 처리 테크닉을 활용하기 위해서는 전체 훈련 집합을 한 번에 처리해야 한다. 큰 데이터 집합에 대해서는 이러한 방식이 계산적으로 실행하기에 너무 복잡할 수도 있다.
데이터 집합이 충분히 클 경우 순차적 알고리즘을 활용하는 것이 유용할 수도 있다. 이를 온라인 알고리즘이라고도 한다. 순차적 알고리즘에서는 한 번에 하나의 데이터 포인트를 고려하여 모델의 매개변수들은 그때마다 업데이트된다.
확률적 경사 하강법, 순차적 경사 하강법을 적용하여 순차적 학습 알고리즘을 구현할 수 있다.
만약 여러 데이터 포인트들에 대한 오류 함수의 값이 데이터 포인트 각각의 오류 함수의 값을 합한 것과 같다면,
E = SUM(E_n)
확률적 경사 하강법을 이용해서 패턴 n 이 등장한 후의 매개변수 벡터 w 를 다음과 같이 업데이트 할 수 있다.

여기서 r 은 반복수를, n 은 학습률을 의미한다.
시작 시 w 의 값을 어떤 시작 벡터 w^(0) 으로 초기화한다.
제곱합 오류 함수의 경우의 위 식은 다음과 같다.
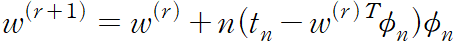
phi_n = phi(x_n) (기저함수) 이다. 이를 최소 제곱 평균 알고리즘이라 한다.
'패턴인식과 머신러닝' 카테고리의 다른 글
| 3.2 편향 분산 분해 (0) | 2023.06.25 |
|---|---|
| 3.1.4 정규화된 최소 제곱법 (0) | 2023.06.25 |
| 3.1.2 최소 제곱의 기하학적 의미 (0) | 2023.06.25 |
| 3.1.1 최대 가능도와 최소 제곱 (0) | 2023.06.24 |
| 3.1 선형 기저 함수 모델 (0) | 2023.06.24 |



