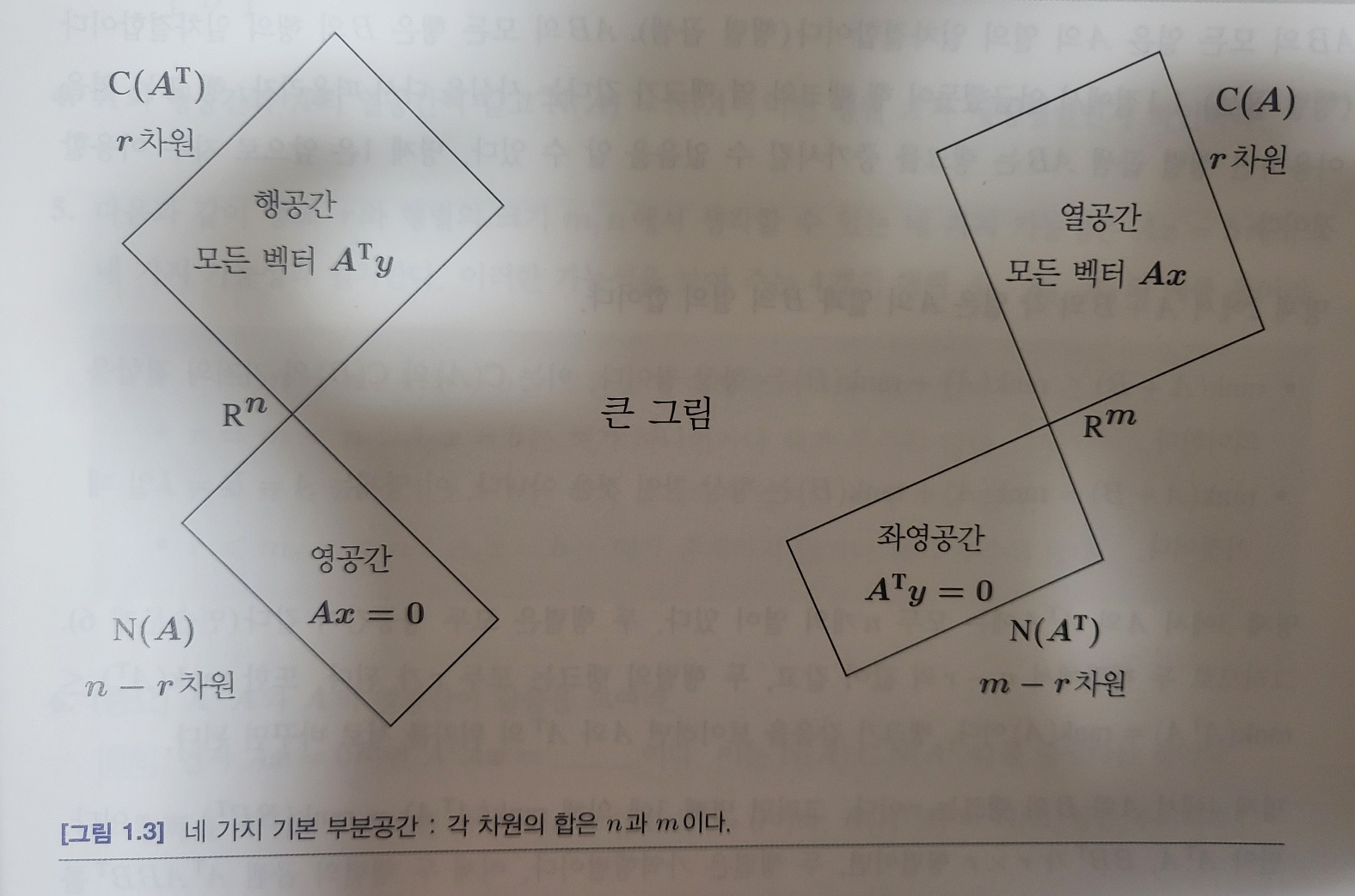
선형대수학의 큰 그림을 그려보고자 한다. 이 그림은 모든 m,n 행렬 A 에서 4 개의 부분공간, 즉 2개의 R^m 부분공간과 2개의 R^n 부분공간이 어떻게 유도되는지를 보여준다.
예제 1은 랭크가 1인 행렬 uv^T 이다. 이 행렬의 열공간은 벡터 u 를 지나는 직선이고 행공간은 벡터 v를 지나는 직선이다.
예제 1
A = (1,2)(3,6) = uv^T 에서 m=2, n=2 이다. R^2 의 부분공간을 생각해보자.
- 열공간 C(A) 는 u = (1)(3) 을 지나는 직선이다. 행렬 A의 2 열 (2)(6) 은 이 직선 위에 있다.
- 행공간 C(A^T) 는 v = (1)(2) 를 지나는 직선이다. 행렬 A의 2행은 이 직선 위에 있다.
- 영공간 N(A) 는 x = (2)(-1) 을 지나는 직선이다. 따라서 Ax = 0 이다.
- 좌영공간 N(A^T)는 y=(3)(-1) 을 지나는 직선이다. 따라서 A^Ty = 0 이다.

- 영공간 C(A) 는 행렬 A의 모든 열의 일차결합을 포함한다.
- 행공간 C(A^T) 는 행렬 A^T 의 모든 열의 일차결합을 포함한다.
- 영공간 N(A) 는 Ax = 0 의 모든 해를 포함한다.
- 좌영공간 N(A^T) 는 A^Ty=0 의 모든 해를 포함한다.
예제 2
행렬 B = (1,-2,-2)(3,-6,-6) 에서 m=2, n=3 이다. 따라서 행렬 B의 기본 부분공간은 R^3 과 R^2 의 부분공간이다.
행렬 A와 B 를 비교하면 두 가지 부분공간은 바뀌며, 두 가지 부분공간은 바뀌지 않는다. 행렬 B의 열공간은 R^2 의 부분공간이며 행렬 A 의 열공간과 기저 벡터가 같다. 그러나 행렬 B 의 열개수는 n=3 이고, 3차원 공간 R^3 이다.
여전히 행공간에는 하나의 v 만 있다. 행렬 B 의 두 행은 같은 방향이므로 랭크 r = 1 이다.
n=3 개의 미지수와 하나의 독립인 일차방정식으로 이루어진 연립일차방정식 Bx = 0 에는 3-1 = 2 개의 일차독립인 해 x1 과 x2가 있다. 모든 해는 영공간에 포함된다.
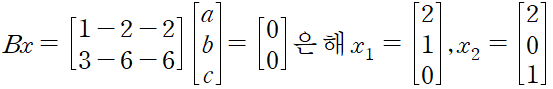
영공간 N(B) 는 R^3 에서 하나의 평면이다. 이 평면에서는 서로 수직인 정교기저인 벡터 v2 와 v3 를 확인할 수 있다. 각각 이루는 각도는 90 이다.

셈 법칙 : r 개의 독립인 일차방정식으로 이뤄진 Ax = 0 에는 일차독립인 해가 n - r 개 있다.
예제 3
5개의 일차방정식, 이 방정식에는 4개의 미지수가 있다. Ax = b 에서 행렬 A는 그래프에서 5*4 결합행렬이다.
이 결합행렬의 네 가지 기본 부분공간을 이해한다면 선형대수학의 중심 개념을 포착한 것이다.
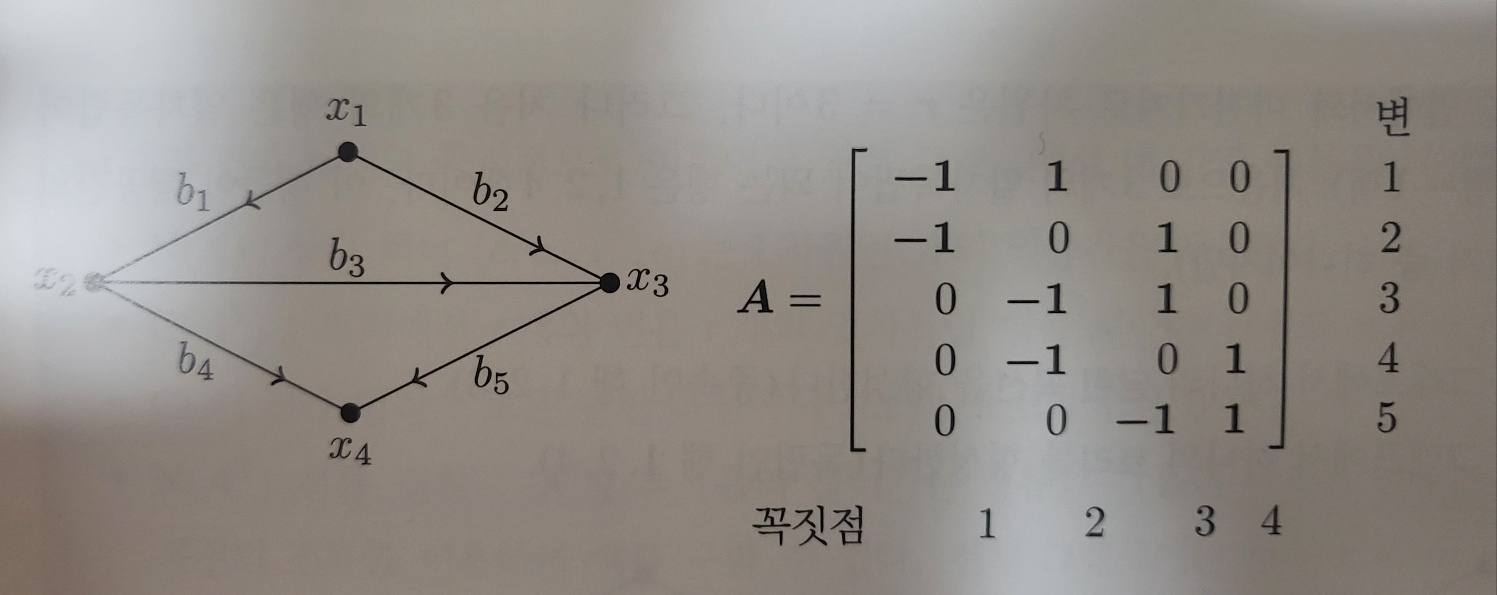
위 그래프의 변은 5 개이고 꼭짓점은 4 개이다. A는 이 그래프의 5*4 결합행렬이다.
영공간 N(A)
영공간을 찾기 위해 5개의 방정식에서 b=0 으로 둔다. 그러면 4개의 미지수 x1~x4 는 같은 값 c 를 가지는 것을 알 수 있다.
벡터 x = (1,1,1,1) 과 모든 벡터 x = (c,c,c,c) 는 Ax=0 의 해가 된다.
이 영공간은 R^4 에서 직선이다. 특수해 x = (1,1,1,1) 은 영공간 N(A) 의 기저이고, N(A) 의 차원은 1이다. (기저 벡터가 한 개이면 직선을 의미하며, 직선의 차원은 1이다.)
n-r=1 에서 행렬 A 의 랭크가 3임을 확인하라 수 있다. 랭크 r = 3 이므로 4개의 부분공간의 차원을 알 수 있다.
- A 의 행공간의 차원 = r = 3
- A 의 열공간의 차원 = r = 3
- A 의 영공간의 차원 = n - r = 1
- A^T 의 영공간의 차원 = m - r = 2
열공간 C(A) : r = 3 개의 일차독립인 열이 존재해야 한다. 이를 확인하기 위한 가장 빠른 방법은 처음 3 개의 일차독립인 열이 존재해야 한다.
일차독립은 Ax=0 의 해가 단 하나 (x1, x2, x3) = (0, 0, 0) 만 존재함을 의미한다.
결합행렬 A의 4 열은 다른 세 열의 합에 -1 을 곱하여 얻는다.
행공간 C(A^T)
열에서와 마찬가지로 차원은 r = 3 이다. 그러나 처음 3 개의 행은 일차독립이 아니다. 처음으로 3개의 일차독립이 되는 행은 1,2,4 행이다. 이 행들이 행공간의 기저이다. ( 많은 기저 공간 중 하나)
- 변 1,2,3 은 그래프에서 하나의 닫힌 곡선을 형성한다. (종속인 행 1,2,3)
- 변 1,2,4 은 그래프에서 하나의 트리를 형성한다. (독립인 행 1,2,4)
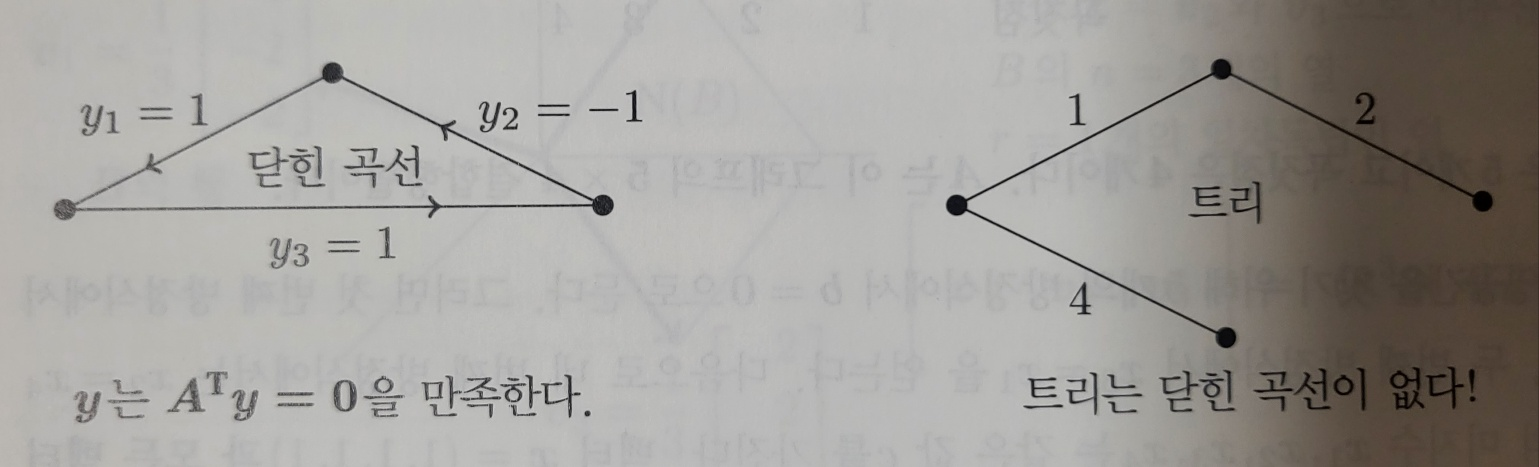
좌영공간 N(A^T)
이제 A^Ty=0 의 해를 구해본다. 행의 일차결합은 0이다. 이미 3 행이 2 행에서 1 행을 뺀 것 임을 알고 있으므로 하나의 해 y=(1,-1,1,0,0) 을 쉽게 찾을 수 있다. y 는 그래프에서 위쪽 닫힌 곡선을 얻을 수 있다.
또 하나의 y 는 그래프에서 아래쪽 닫힌 곡선에서 얻을 수 있다. y=(0,0,-1,1,-1) 은 A^Ty=0 의 일차독립인 해이다.
방정식 A^Ty=0 은 그래프에서 다섯 개의 변 위에 있는 전류 y1~y5 를 제공한다. 닫힌 곡선 주위의 흐름은 키르히호프의 전류 법칙을 따른다. 이 이론은 전기 회로에 적용한다.
그래프는 응용 이산수학에서 가장 중요한 모델이다. 그래프 이론에서 나오는 결합행렬 A 와 A^T 를 잘 이해하자.
m 개의 변과 n 개의 꼭짓점으로 이뤄진 연결 그래프에서 네 가지 부분공간 (결합행렬은 A)
- N(A) : 상수 벡터는 1차원인 A 의 영공간을 제공한다.
- C(A^T) : 트리에서 r 개의 변은 r 개의 일차독립 행은 제공한다.
- C(A) 전압 법칙 : 모든 닫힌 곡선에서 Ax 요소의 합은 0이다.
- N(A^T) 전류 법칙 : A^Ty = 흘러 들어가는 전류 - 흘러 나가는 전류 = 0 은 닫힌 곡선의 전류를 이용하여 해를 구할 수 있다. 전체 그래프에는 m-r=m-n+1 개의 독립인 부분 닫힌 곡선이 존재한다.
'선형대수학' 카테고리의 다른 글
| 1.4.1 소거법을 이용한 Ax = b 의 풀이 (1) | 2022.12.09 |
|---|---|
| 1.3.1 AB 와 A+B 의 랭크 (1) | 2022.12.09 |
| 1.2.2 열과 행의 곱셈에 대한 이해 (0) | 2022.12.08 |
| 1.2.1 AB=(랭크 1 행렬의 합) (1) | 2022.12.08 |
| 1.2 행렬 곱셈 AB (2) | 2022.12.08 |
