A 가 정사각행렬일 때, A^-1 과 A 를 곱하면 I 가 되는 동일한 크기의 역행렬 inverse matrix A^-1 을 살펴보자.
이 곱은 항등 행렬이 되며, 따라서 모든 벡터의 변화를 무효가 되게 한다. 따라서 A^-1Av = v 이다. 하지만 A^-1 는 존재하지 않을 수도 있다.
행렬에서는 주로 벡터 v 를 곱한다. Av = b 에서 A^-1 을 곱하면 A^-1Av = A^-1 b 가 된다. 이는 v = A^-1 b 이다.
곱 A^-1 A 는 수를 곱한 다음 다시 그 수로 나누는 것과 같다. 수는 역수가 된다.
A^-1 가 존재하여 다음을 만족할 때, 행렬 A 를 가역 invertible 이라고 한다. A^-1A = I, AA^-1 = I
모든 행렬이 역행렬을 갖는 것은 아니다. A^-1 에 관한 여섯 개의 성질이 있다.
- A^-1 이 존재하는 것과 소거가 n 개의 피봇을 만드는 것은 동치이다. 소거는 직접적으로 A^-1 을 사용하지 않으면서 Av = b 를 푼다.
- 행렬 A 는 서로 다른 역행렬을 가질 수 없다.
- A 가 가역이면 Av = b 의 유일한 해는 v = A^-1 b 이다.
- 영벡터가 아닌 벡터 v 에 대해 Av = 0 이라고 하자. 그러면 A 는 역행렬을 가질 수 없다. 그 어떤 행렬도 0을 v로 되돌릴 수 없다.
- A 가 가역이면 Av 는 오직 0 인 해 v = A^-1 0 = 0 을 갖는다.
- 2*2 행렬이 가역인 것과 ad - bc가 0이 아닌 것은 동치이다. 이 수 ad - bc 는 A 의 행렬식 determinant 이다. 행렬은 행렬식이 0이 아닐 때 가역이다. 이때 A^-1 가 항상 행렬식으로 나눠지는 형태를 갖는 것은 아니다.
- 대각 행렬은 모든 대각성분이 0이 아니라는 가정 하에 역행렬을 갖는다.

곱 AB의 역행렬
0이 아닌 a와 b 에 대해 a+b 는 역수를 가질 수도, 안 가질 수도 있다. 두 수 a = 3, b = -3 은 각각 역수 1/3, -1/3 을 갖는 반면 합 0은 역수를 갖지 않는다. 하지만 이들의 곱은 역수를 갖는다.
행렬에섣 비슷하다. 곱 AB 가 역행렬을 갖는 것과 두 개의 인자 A 와 B 가 각각 가역인 것은 동치이다.
행렬 A 와 B 가 가역일 때, AB 도 가역이다. 곱 AB의 역행렬은 다음과 같다. (AB)^-1 = B^-1 A^-1
AB의 역행렬 (AB)(B^-1 A^-1) = AIA^-1 = I
괄호를 움직여 BB^-1 를 먼저 곱했다. 이와 비슷하게 B^-1 A^-1 와 AB 의 곱은 I 와 같다. 이는 역은 반대 순서로 온다는 수학의 기본적인 법칙을 보여준다.
가우스-조던 소거법으로 계산한 A^-1
Av = b 의 방정식은 v = A^-1 b 로 풀 수 있다. 하지만 A^-1 을 계산하고 이를 b 에 곱하는 것은 비효율적이다. 가우스-조던 소거법은 v로 직접 간다.
이제부터 소거 또한 A^-1 을 찾을 수 있다는 것을 살펴본다.
A는 A^-1 의 첫 번째 열 v_1 과 곱하면 I 의 첫 번째 열 e_1 이 된다. 이는 방정식 Av_1 = e_1 = (1,0,0) 이다. 이때 두 개의 방정식이 더 있을 것이다. A^-1 의 각 열 v_1, v_2, v_3 은 A 와 곱하면 I 의 열이 된다.
가우스-조던 원리는 AA^-1 = I 를 푸는 것, A^-1 의 각 열을 찾는다.
일반적으로 첨가 행렬 augmented matrix [A b] 는 추가된 열 b를 더 갖고 있다. 첨가 행렬은 블록 행렬 [A I] 이다.

이로써 A^-1 의 절반까지 구했다. 처음 세 열의 행렬은 U 이다. 피봇 2, 3/2, 4/3 은 이들의 대각선에 있다. 가우스는 역대입법으로 마무리할 것이고, 조던의 아이디어는 소거를 계속하는 것이다.
위의 행에서 행이 빼지고, 피봇 위에 0을 만든다.
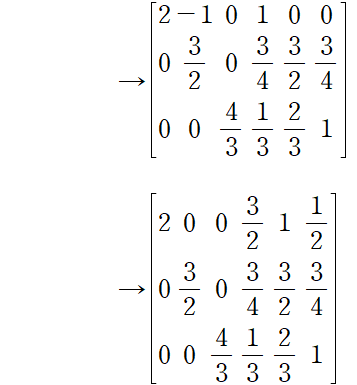

- A 가 주대각성분을 가로질러 대칭이면 A^-1 도 그렇다.
- A 가 삼중대각 ( 0이 아닌 오직 세 개의 대각성분) 이다. 하지만 A^-1 은 full matrix 이다. 이는 우리가 역행렬을 계산하지 않는 다른 이유이다.
- 피봇의 곱은 A 의 행렬식이다.
A^-1 은 행렬식으로 나누는 나눗셈을 포함한다.
가우스-조던 소거법은 A^-1 의 계산량이 많은 이유를 보여준다. 우리는 n 개의 열에 대해 n 개의 방정식을 풀어야 한다.
A^-1 없이 Av = b 를 풀기 위해 열 b 를 이용해서 열 v 를 찾는다.
비가역과 가역
핵심 질문은 어떤 행렬이 역행렬을 갖는가? 이다.
A^-1 은 A 가 꽉 찬 n 개의 피봇을 가질 때 존재한다. 이 때 우리는 가우스-조던 소거법을 증명할 수 있다.
'미분방정식' 카테고리의 다른 글
| 6.1 고윳값에 대한 소개 - det(A - lamda I) = 0 으로부터 고윳값 찾기 (0) | 2022.12.15 |
|---|---|
| 6.1 고윳값에 대한 소개 (0) | 2022.12.15 |
| 4.5 대칭 행렬과 직교 행렬 (1) | 2022.12.15 |
| implement_matrix multiplication (0) | 2022.12.14 |
| 4.1 선형 방정식의 두 그림 (1) | 2022.12.14 |


