고윳값은 n 개의 미분방정식으로 이뤄진 시스템의 핵심이다. dy/dt = ay 는 dy/dt = Ay 가 된다. 이제 A 는 행렬이고 y 는 벡터이며, 벡터 y 는 시간에 따라 변한다. 다음 2개의 방정식으로 이뤄진 시스템과 2*2 행렬 A 를 살펴본다.

이 두 식에서 y_1, y_2 에 대해 연결된 시스템 y' = Ay 를 어떻게 풀어야 하는가? 좋은 방법은 문제를 분해하는 근을 찾는 것이다. 우리는 증각하거나 감소하는 y_1, y_2 를 원한다.

벡터 x = (a,b) 는 고유벡터라 부르고, 증가율 lamda 는 고윳값이다.
여기서는 식 1 의 행렬에 대한 x 와 lamda 의 의미를 살펴본다.
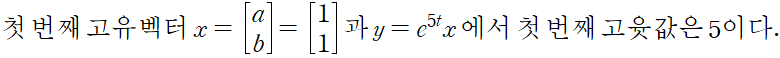


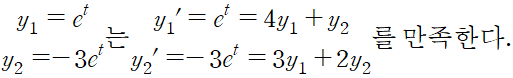
임의의 c_1, c_2 에 대해 x 와 lamda 를 결합하면 y' = Ay 의 완전해를 구할 수 있다.

이 고윳값들은 행렬의 중심을 살펴보는 새로운 방법이다.
'미분방정식' 카테고리의 다른 글
| 6.1 고윳값에 대한 소개 (행렬의 거듭제곱) (0) | 2022.12.15 |
|---|---|
| 6.1 고윳값에 대한 소개 - det(A - lamda I) = 0 으로부터 고윳값 찾기 (0) | 2022.12.15 |
| 4.5 대칭 행렬과 직교 행렬 (1) | 2022.12.15 |
| 4.4 역행렬 (0) | 2022.12.15 |
| implement_matrix multiplication (0) | 2022.12.14 |


