A 의 고윳값을 알 때, 모든 거듭제곱 A^k 의 고윳값과 평행이동 A + cI 와 A 의 모든 함수를 알게 된다.
A 의 각 고유벡터도 역시 A^k, A^-1, A + cI 의 고유벡터와 같다.
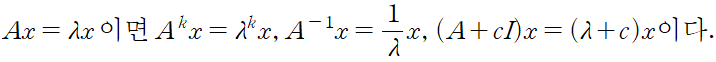
A 와 Ax = ladma x 의 곱인 A^2x 에서 다시 시작해보자. 그러면 A lamda x 는 임의의 수 lamda 에 대해서 lamda A x 와 같고 이는 lamda^2 x 이다.
차수가 더 높은 A^k x 에 대해서 Ax = lamda x 에 A 를 계속 곱한다. 우리는 점차 A^k x = lamda^k x 에 도달한다. A^-1 의 고윳값에 대해 먼저 A^-1 을 곱하고 lama 로 나눈다.
A^-1 의 고윳값에 대해 먼저 A^-1 을 곱하고 lamda 로 나눈다.

A^-1 이 존재한다고 가정, 만약 A 가 가역행렬이면 lambda 는 절대로 0이 될 수 없다.
비가역 행렬은 고윳값 lambda = 0 을 갖는다.
A 에서 A+cI 로의 평행이동은 모든 고윳값에 c 를 더할 뿐이다. x 를 변화시키지 않는다.


무한급수도 행렬을 생성한다는 것을 증명하였다.
100개의 행렬을 일일히 곱하지 않고도 lambda=1 과 고유벡터를 사용해여 A^100 을 찾았다. A 의 고윳값은 1과 1/2 이므로 A^100 의 고윳값은 1과 (1/2)^100 이다. 이 마지막 수는 매우 작으며 A^100 의 소숫점 아래 30 자리에서도 이 숫자를 볼 수 없다.
v=(0.8,0.2) 와 같은 다른 벡터에 어떻게 A^99 를 곱할 수 있는가? 이 벡터 v 는 고유벡터가 아니지만, 고유벡터의 결합이다. 임의의 벡터 v 를 고유벡터로 사용해서 표현하는 것, 이것이 주요 아이디어이다.

벡터에 A 를 곱할 때, 각각의 고유벡터에 대응하는 고윳값과 곱한다.
AB 와 BA 의 고윳값은 같다.
'미분방정식' 카테고리의 다른 글
| 6.2 행렬의 대각화 (0) | 2022.12.15 |
|---|---|
| 6.1 고윳값에 대한 소개(행렬식) (0) | 2022.12.15 |
| 6.1 고윳값에 대한 소개 - det(A - lamda I) = 0 으로부터 고윳값 찾기 (0) | 2022.12.15 |
| 6.1 고윳값에 대한 소개 (0) | 2022.12.15 |
| 4.5 대칭 행렬과 직교 행렬 (1) | 2022.12.15 |


