x 가 고유벡터일 때, A 를 곱하는 것은 Ax = lambda x 와 같이 그저 수 lambda 를 곱하는 것이다.
서로 연관된 시스템 대신에 우리는 독립적인 고유벡터를 살펴볼 것이다. 이는 대각성분이 아닌 성분과 연관이 없는 대각 행렬을 갖는 것과 같다. 대각 행렬의 경우 100 제곱은 쉽다.
고유벡터를 적절하게 사용하면 행렬 A 는 대각 행렬 A 로 바뀐다. 이는 주요 아이디어의 행렬 형태이다.
대각화
n*n 행렬 A 가 n 개의 선형독립 고유벡터 x_1, ..., x_n 을 갖는다고 가정, 이들을 고유벡터 행렬 V 의 열들로 넣자. 그러면 V^-1 A V 는 고윳값 행렬 ∀ 이고, ∀ 는 대각행렬이다.

위 식에서 행렬 A 는 대각화 되었다. 우리는 고윳값 행렬에 대해 대문자 lambda 를 사용하는데, 이는 이 행렬의 대각성분은 lambda 들이기 때문이다.
증명
V 의 열인 행렬의 고유벡터를 A 에 곱한다. 그러면 AV 의 첫 번째 열은 Ax_1 이고 이는 lambda_1 x_1 이다. V 의 각 열은 고윳값 lambda 에 의해 곱해진다.


lambda_1 은 첫 번째 열 x_1 에 곱해진다.
AV=VA 는 V^-1 A V = ∀ 또는 A = V ∀ V^-1 이다.
A와 ∀ 는 같은 고윳값을 갖지만, 고유벡터들은 다르다. 원래의 고유벡터의 일은 A 를 대각화하는 것이었다. V 의 고유벡터들은 A = V∀V^-1 을 만족시킨다.
1차 차분과 미분방정식의 풀이
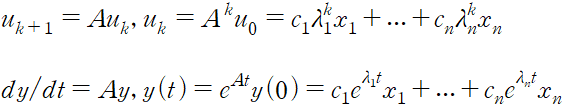
두 문제에 대한 아이디어는 다음과 같다. n 개의 독립적인 고유벡터들은 기저를 형성한다. 우리는 u 와 y(0) 를 고유벡터의 결합으로 쓸 수 있다. 그러면 k 가 증가하고 t 가 증가할 때, 각각의 고유벡터를 따른다.

예제
대각선 성분이 lambda 인 삼각 행렬 A 가 있다. (lambda = 1, 6)
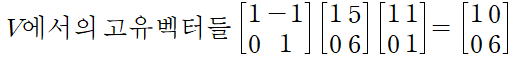
A 와 A^2 의 같은 고유벡터들은 V 안에 있고, 고윳값의 제곱은 A^2 에 있다.

k = 1 이면 A 를, k = 0 이면 A^0 = I 를 얻는다. k = -1 이면 우리는 역행렬 A^-1 을 얻을 수 있다. 또한 k = 2 일 때, A^2=[1 35:0 36] 이 어떻게 이 식에 적합한지 확인할 수 있다.
A 를 다시 사용하기 전에 주목해야 할 네 가지 사항
- 고윳값들이 서로 다를 때, 고유벡터들은 독립이다. 종복된 고윳값이 없는 임의의 행렬들은 대각화가 가능하다.
- 고유벡터에 0이 아닌 임의의 상수를 곱할 수 있다. Ax = lambda x 는 여전히 참이다. 고유벡터를 나눠서 단위벡터를 만들 수 있다.
- V 안의 고유벡터들은 A 안의 고윳값과 같은 순서로 이뤄져 있다.
- 중복된 고윳값에 대해 살펴보자. 어떤 행렬들은 매우 작은 수의 고유벡터를 갖는다. 이 행렬들은 대각화할 수 없다. 여기서의 문제점은 lambda 의 값이 반복된다는 것이다.
가역성과 대각화 가능성 사이에 연관 관계가 없음을 기억하자
- 가역성은 고윳값과 관련이 있다.
- 대각화 가능성은 n 개의 독립적인 고유벡터를 필요로 한다.
각 고윳값은 적어도 하나의 고유벡터를 갖는다.
A - lambda I 는 비가역 행렬이다. 이때 (A - lambda I)x = 0 이 x = 0 이 된다면 lambda 는 고윳값이 아니다.
예제
이전 예제 마르코프 행렬 A 는 lambda = 1, 0.5 를 가졌다. 고윳값이 행렬 A 에 있는 A = V∀V^-1 은 다음과 같다.

고유벡터 (0.6, 0.4) 와 (1,-1)은 V 의 두 열이며 이는 A^2 의 고유벡터이기도 하다. A^2 이 어떻게 같은 V 를 갖는지와 A^2 의 고윳값 행렬이 ∀^2 임에 주의

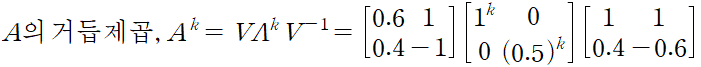
k 가 커짐에 따라 (0.5)^k 은 작아지며 극한에서 이는 완전히 사라진다. 각 성분의 극한값으로 이뤄진 행렬이 A^(INF)

'미분방정식' 카테고리의 다른 글
| 6.3 선형시스템 y'=Ay (1) | 2022.12.16 |
|---|---|
| 6.2 행렬의 대각화(행렬의 거듭제곱 A^k) (0) | 2022.12.16 |
| 6.1 고윳값에 대한 소개(행렬식) (0) | 2022.12.15 |
| 6.1 고윳값에 대한 소개 (행렬의 거듭제곱) (0) | 2022.12.15 |
| 6.1 고윳값에 대한 소개 - det(A - lamda I) = 0 으로부터 고윳값 찾기 (0) | 2022.12.15 |



