6.1 고윳값에 대한 소개(행렬식)

행렬이 역행렬을 갖지 않을 때, 행렬식은 0 이다. 이는 고윳값 방정식 det(A-lambda I) = 0 이다. A 가 가역 행렬일 때, A^-1 의 행렬식은 1/(det A) 이다. A^-1 의 모든 성분은 두 행렬식의 비율이다.

det(A-lambda I) = 0 이 갖는 어려움은 n*n 행렬식이 n! 개의 항과 관련이 있다는 것이다. n = 3 이면 6개의 항이 있는데, 이 중 3개의 항은 양의 부호를, 3개의 항은 음의 부호를 갖는다. 이 6개의 각각의 항은 모든 행과 모든 열로부터의 수 한 개를 포함한다.

행렬식의 성질

1. 다른 행에서 한 행의 배수를 빼는 것은 det A 를 변화시키지 않는다.
2. 두 행의 위치를 바꿀 때, 행렬식의 부호가 바뀐다.
3. A 가 삼각 행렬이면 det A = 대각성분들의 곱이다.
4. AB 의 행렬식은 det A 와 det B 의 곱과 같다.
5. A^T 의 행렬식은 A 의 행렬식과 같다.

1~3 을 조합하면 행렬식이 소거법으로부터 어떻게 나오는지 알 수 있다.

행렬식은 +-(피봇들의 곱)과 같다.

1. 은 행의 위치를 바꾸지 않는 한 A 와 U 는 같은 행렬식을 갖는다는 것을 의미한다.
2. 행의 위치를 홀수 번 바꾸면 det A = -det U 가 됨을 의미한다.
3. det U 는 주요 대각성분의 피봇들의 곱임을 의미한다.

소거법을 통해 A 를 U로 바꿀 때, det A = +1 (피봇들의 곱) 임을 얻는다. 이는 모든 수치 소프트웨어를 사용해 det A 를 계산하는 방법이다. 

A^-1 의 열들을 찾기 위해 AA^-1 = I 를 풀어보자. 이는 가우스-조던 소거법인데, I 의 각각의 열 b 에 대해서 A^-1 의 열 v 를 찾기 위해 Av = b 를 푼다. b 가 I 의 열인 이 특별한 경우, 크래머의 법칙에서 수 det B_j 를 여인수 cofactor 라 부른다. 여인수들은 크기가 (n-1) 인 행렬식으로 줄어드는데, 이는 b 가 매우 많은 0을 갖고 있기 때문이다. A^-1 의 모든 성분은 A 의 여인수를 A 의 행렬식으로 나눈 것이다.

행렬의 대각합 trace 를 소개하고 실수 행렬이 허수 고윳값과 고유벡터를 가질 수 있다는 것을 보여주기 위해 세 개의 행렬을 확인

예제

S = (2,1)(1,2) 의 고윳값과 고유벡터를 찾아라

x = (1,1) 은 Sx = (3,3) 과 같은 방향이라는 것을 확인할 수 있다. 그러면 x 는 lambda = 3 인  S 의 고유벡터이다. 우리는 S-lambda I 가 비가역 행렬이기를 바란다.

3이 S 의 행렬식임에 주목, 그리고 4는 S 의 대각합이다. 이는 lambda 들의 합과 같다.

각 고윳값은 다음의 고유벡터를 갖는다.

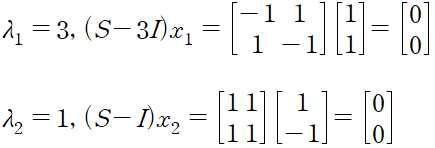
고윳값은 실수이고, 고유벡터는 서로 수직이다. 대칭 행렬 symmetric matrix 에 대해서 이 성질들은 항상 동반된다.

A^T = -A 인 비대칭 행렬이 있다. 이 행렬은 모든 실수 벡터를 a = 90 만큼 회전시킨다. 실수 벡터는 이 회전 행렬의 고유벡터가 될 수 없는데, 이는 회전 행렬이 그들의 방향을 변화시키기 때문이다.

예제

이 실수 행렬은 허수 고윳값 i, -i 와 복소수 고유행렬을 갖는다.

이 행렬식은 lambda^2+1 은 lambda=-i 일 때 0이다. 고유벡터는 (1, -i) 와 (1,i) 이다.

아무튼 이 두 복소 벡터 x_1, x_2 는 회전되지 않는다. 

고윳값의 곱은 1을, 합은 0이 된다. 이는 A 의 대각성분을 더한 값과 같다. (0)

고윳값의 곱 = 행렬식, 고윳값의 합 = 대각합

고윳값의 합은 특히 행렬과 대각합이 lambda_1,2 를 완벽하게 결정하는 2*2 행렬에서 중요하다. 이제 임의의 각 a 에 대한 평면에서의 회전을 살펴본다.

예제

회전은 직교 행렬 Q 로부터 온다. 이때 lambda_1 = e^ia 이고 lambda_2 = e^-ia 이다.

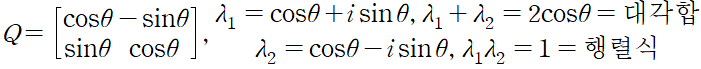
여기서 lambda_1,2 를 곱하면 cos^2 a + sin^2a = 1 을 얻는다. 극좌표 형식에서 e^ia 와 e^-ia 의 곱은 1이다. Q 의 고유벡터는 모든 회전 각 a 에 대해서 (1, -i) 와 (1, i) 이다.

큰 행렬에 대해서 고윳값과 고유벡터를 찾는 것은 쉽지 않다. 식 det(A-lambda I) = 0 은 2*2 행렬과 3*3 행렬에 대해서 더 혹은 덜 제한적이다. 큰 행렬에 대해서 우리는 고윳값을 변화시키지 않고 점진적으로 이 행렬을 삼각 행렬로 만들 수 있다. 

삼각 행렬에 대해서 고윳값은 대각성분들이기 때문이다.