회귀 문제에서의 결정 이론, 곡선 피팅 문제가 회귀 문제에 해당한다. 회귀 문제의 결정 단계에선느 각각의 x 에 대해서 t 의 추정값 y(x) 를 선택해야 한다. 이과정에서 손실 L(t,y(x)) 가 발생한다고 가정해본다.
그러면 평균 손실은 다음과 같이 주어진다.

회귀 문제에서 일반적으로 손실 함수로서 사용하는 것은 L(t,y(x))=(y(x)-t)^2 로 주어지는 제곱 손실이다. 이 경우 기대 손실은 다음과 같다.

우리의 목표는 E[L] 을 최소화하는 y(x) 를 선택하는 것이다. 만약 완벽하게 유연한 함수 y(x) 를 결정할 수 있다고 가정하면, 변분법을 사용해서 다음과 같이 적을 수 있다.

y(x) 에 대해서 해를 구하고 확률의 합과 곱의 법칙을 적용하면 다음을 얻게 된다.

위 식은 x가 주어졌을 때의 t 의 조건부 평균으로써 회귀 함수라고 한다. 이 경우 최적의 해는 조건부 평균 y(x)=E_t[t|x] 다.
이 결과는 약간 다른 방식을 통해서도 도출할 수 있다. 최적의 해가 조건부기댓값이라는 지식을 바탕으로 제곱항을 다음과 같이 전개할 수 있다.

이 전개 결과를 손실 함수에 대입하고 t 에 대해 적분하면 교차항들이 사라지게 된다. 그 결과로 다음 형태의 손실 함수를 얻을 수 있다.

우리가 찾고자 하는 함수 y(x) 는 첫 번째 항에만 있는데, y(x) 가 E[t|x] 일 때 이 항은 최소화되어 항 자체가 사라지게 된다. 이는 앞서 도출한 결과와 동일
즉, 최적의 최소 제곱 예측은 조건부 평균으로 주어진다는 것을 보여준다. 두 번째 항은 t 에 대한 분포의 분산을 계산하고, 이를 x 에 대해 평균을 낸 것이다. 이 항은 표적 데이터가 가지고 있는 내재적인 변동성을 표현하는 것으로, 노이즈라고 해석할 수 있다. 이 항은 y(x) 에 대해 독립적이며, 따라서 절대로 더 이상 줄일 수 없는 손실 함수의 최솟값에 해당한다.
회귀 문제에서도 적절한 확률값들을 먼저 구한 후, 최적의 결정을 내릴 수도 있고, 결정을 직접 내리는 모델을 만들 수도 있다. 회귀 문제를 풀기 위한 세 가지 서로 다른 방식은 다음과 같다.
a
결합 밀도 p(x,t) 를 구하는 추론 문제를 풀어낸다.다음에 이를 정규화하여 조건부 밀도 p(t|x) 를 구하고 최종적으로 조건부 평균을 구한다.
b
조건부 밀도 p(t|x) 를 구하는 추론 문제를 풀고 조건부 평균을 구한다.
c
훈련 데이터로부터 회귀 함수 y(x) 를 직접 구한다.
회귀문제의 손실 함수로제곱 손실 이외의 다른 것을 사용하는 것도 가능하다. 실제로 제곱 손실이 상당히 좋지 않은 결과를 가져오기 때문에 더 복잡한 접근법을 사용해야 하는 경우가 종종 있다.
조건부 분포 p(t|x) 가 다봉 분포인 상황이 이 중 하나이다. 역 문제의 해를 구할 때 이런 상황이 종종 발생한다.
제곱 손실을 일반화한 예시인 민코프스키 손실의 기댓값은 다음과 같이 주어진다.
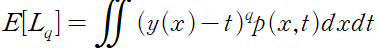
q = 2 일 경우 제곱 손실에 해당한다. q = 1 일 때는 조건부 중간값, 0일 때는 조건부 최빈값으로 주어지게 된다.
'개념 정리' 카테고리의 다른 글
| 정보 이론(상대적 엔트로피와 상호 정보량) (1) | 2022.12.20 |
|---|---|
| 정보 이론 (1) | 2022.12.20 |
| 결정 이론(추론과 결정) (0) | 2022.12.19 |
| 결정 이론(거부 옵션) (0) | 2022.12.19 |
| 결정 이론(기대 손실의 최소화) (0) | 2022.12.19 |


