속도함수만 주어졌을 때 위치함수를 구하는 방법
- 속도함수의 부정적분을 구한다.
- 이동하는 물체의 출발점을 찾는다.
- 초기 조건을 부정적분 등식에 대입해 부정적분 상수를 구한다.
부정적분
y=f(x) 라는 함수가 주어졌을 때, 함수 F(x) 라 함은 f(x) 의 부정적분으로서 다음의 조건을 충족한다.

int(f(x) dx) 는 f(x) 의 부정적분을 의미하고, F(x)+C 와 같다. F(x) 는 부정적분이고, C 는 임의의 상수이다.
임의의 상수 C 는 초기 조건을 알면 구할 수 있다.
속력이 dx/dt = 60 - 4t 일 경우,
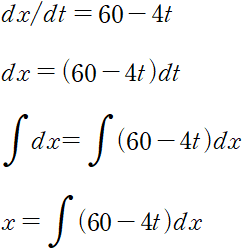
적분에서의 합의 법칙
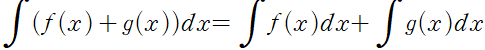
두 함수의 합인 함수의 적분값은 각각의 함수의 적분값을 합한 것과 같다.
적분에서의 곱의 법칙
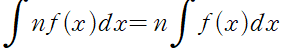
완전적분의 법칙

적분에서의 거듭제곱의 법칙
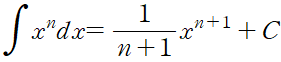
치환적분법
u 가 x 에 대한 함수일 경우 int(u^n dx) 와 같은 형식의 적분을 구하기 위해서는 거듭제곱의 법칙을 직접 적용할 수 없고 반드시 dx 를 du 로 변환시켜야 한다. 우선 u 의 도함수 du/dx 를 구한 후, 이것을 미분표현법으로 바꾼다.
다음으로 dx = (dx/du)du 로 치환시키면 적분은 이렇게 구해질 수 있다.

만약 dx/du 가 상수일 경우, 이 상수는 적분기호 밖으로 빼낼 수 있다.

'미적분' 카테고리의 다른 글
| 8. 적분으로 넓이 계산 (0) | 2022.12.21 |
|---|---|
| 6. 최적값과 상대율 (0) | 2022.12.21 |
| 5. 삼각함수의 도함수 (0) | 2022.12.21 |
| 4. 복잡한 함수의 도함수 (2) | 2022.12.21 |
| 도함수를 이용하여 그래프 그리기 (0) | 2022.12.20 |



