부류 문제의 목표는 입력 벡터 x 가 주어졌을 때 이를 K 개의 이산 클래스들 중 하나에 할당하는 것,
대부분의 문제에서 클래스들은 서로 겹치지 않는다. 즉, 각각의 입력값들은 하나의 클래스에 할당된다. 입력 공간은 결정 경계 또는 결정 표면이라고 불리는 경계를 바탕으로 여러 결정 구역들로 나눠지게 된다.
분류를 위한 선형 모델에 대해 관찰, 선형 모델의 의미는 결정 표면들이 입력 벡터 x 에 대한 선형 함수라는 것이다.
회귀 문제의 경우에는 타깃 변수 t 가 단순히 예측하고자 하는 실수, 분류 문제의 경우 클래스 라벨을 표현하기 위해서 다양한 방식으로 타깃 변수를 사용할 수 있다.
확률적 모델의 경우 두 개의 클래스를 가지는 문제에서 가장 손쉽게 사용할 수 있는 타깃 변수 표현 방법은 단일 타깃 변수를 사용하는 것, K > 2 개의 클래스가 있을 경우에는 원 핫 인코딩을 적용하는 것이 편리하다.
t 는 K 길이의 벡터가 되며, t_j 는 1을 나머지는 0 값을 가지게 될 것이다.
분류 문제를 푸는 방법 중 가장 단순한 방법은 판별 함수를 만들어 활용하는 방식, 판별 함수는 각각의 벡터를 특정 클래스에 직접 바로 배정하는 함수,
또 다른 방법은 추론 단계에서 조건부 확률 분포 p(C_k|x) 를 모델하고 이 분포를 활용하여 최적의 결정을 내리는 방식,
조건부 확률을 결정하는 방법으로
직접 모델하는 것으로 조건부 확률을 매개변수적 모델로 표현하여 최적의 매개변수를 훈련 집합을 통해 찾아내는 방법,
또 다른 방법은 생성적인 방법으로 클래스 조건 밀도와 클래스 사전 확률을 모델한 후 필요한 사후 확률을 베이지안 정리를 이용하여 계산하는 방식,
선형 회귀 모델의 경우에 모델의 예측값 y(x,w) 는 매개변수 w 의 선형함수로 주어진다. 가장 단순한 경우 입력 변수에 대해서도 선형이며, y(x) = wx + w_0 의 형태를 취하게 된다.
ㅎㅏ지만 분류 문제에서는 이산 클래스 라벨값을 예측해 내야 한다.
이를 달성학 ㅣ위해서 w 에 대한 선형 함수를 비선형 함수 f 를 이용하여 변환하는 것을 고려
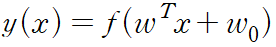
이 f() 를 활성화 함수라고 지칭하며, 이 함수의 역함수를 연결 함수라고 부른다.
결정 경계면은 y(x) = 상수인 경우에 해당한다.
그렇기 때문에 f 가 비선형일지라도 결정 경계면은 x 에 대해 선형 함수다.
회귀 문제에서의 모델과는 달리 매개변수에 대해 선형적이지는 ㅇ낳다. 비선형 함수 때문에 그렇다. 더 복잡한 성질을 가지고 있다.
'패턴인식과 머신러닝' 카테고리의 다른 글
| 4.1.2 다중 클래스 (0) | 2023.06.26 |
|---|---|
| 4.1 판별 함수 (0) | 2023.06.26 |
| 3.2 편향 분산 분해 (0) | 2023.06.25 |
| 3.1.4 정규화된 최소 제곱법 (0) | 2023.06.25 |
| 3.1.3 순차적 학습 (0) | 2023.06.25 |



