머신러닝 통계학

확률 변수와 확률 분포

확률 변수

확률이란 어떤 사건이 일어날 가능성을 수치화시킨 것, 

모든 확률이 0과 1 사이에 있고 모든 사건의 확률을 더하면 1이 된다. 

동전을 던지는 예에서 동전을 던졌을 때 나올 수 있는 경우는 앞면과 뒷면, 이때 발생할 수 있는 모든 경우는 표본 공간이라고 부르고 S라고 표현한다. 

확률 변수 random mvariable 란, 결괏값이 확률적으로 정해지는 변수를 의미, 이는 고정된 값이 아닌 상황에 따라 바뀔 수 있다. 이처럼 확률 변수 X는 확률적 상황에 따라 달라질 숫 있는 변수

변수와 반대되는 개념은 상수, 항상 값이 고정된 수

확률 분포

확률 분포 probability distribution 은 확률 변수가 특정값을 가질 확률 함수를 의미한다. 확률 변수의 값은 확률 분포에 기반해서 얻어진다. 

이산확률 분포와 확률 질량 함수

확률 변수가 가질 수 있는 값을 셀 수 있다는 의미 이산 확률 분포 probability distribution 은 이상 확률 변수의 확률 분포를 의미한다. 

확률 질량 함수 probability mass function 은 이산 확률 변수에서 특정 값에 대한 확률을 나타내는 함수, 

연속 확률 분포와 확률 밀도 함수

연속 확률 변수 continuous random variable 은 확률 변수가 가질 수 있는 값의 개수를 셀 수 없다는 의미, 

확률 밀도 함수 probablity density function 은 연속 확률 변수의 분포를 나타내느 함수 

누적 분포 함수

누적 분포 함수 cumulative distribution function 은 주어진 확률 변수가 특정값보다 작거나 같은 확률을 나타내느 함수

결합 확률 밀도 함수

결합 확률 밀도 함수 joint probablity density function 은 확률 변수 여러 개를 함께 고려하는 확률 분포

확률 변수가 독립일 경우 각각의 확률 변수의 확률 밀도 함수를 곱하는 것과 같다.

독립 항등 분포

두 개 이상의 확률 변수를 고려할 때 각 확률 변수가 통계적으로 독립이고 동일한 확률 분포를 따르는 것

 

모집단과 표본

모집단은 대상 전체를 의미하고 표본은 모집단에서 일부를 추출한 것, 

모집단의 특성을 나타내는 대폿값을 모수라고 하고,

표본의 대폿값을 표본 통계량이라고 한다.

평균과 분산

평균

모평균은 모집단의 평균을 의미

확률에 대한 기댓값

평균이 의미하는 것은 자료 분포의 위치를 설명한다. 이처럼 평균과 같이 그래프의 위치를 결정하는 파라미터를 로케이션 파라미터라고 한다.

분산

분산 variance 데이터가 얼마나 퍼져 있는지를 수치화 한 것, 평균에 대한 편차 제곱의 평균으로 계산된다. 

먼저 모집단의 분산인 모분산 population variance 를 수식으로 나타내면 아래와 같다.

다음과 같은 방법으로도 분산을 구할 수 있다.

 

확률의 경우

표본 분산은 아래와 같이 구한다.

분산의 정의에서 평균에 대한 편차라는 부분은 xi-x 에 해당한다. 분산을 구할 때는 편차 제곱의 합을 n으로 나누는 것이 아닌, n-1로 나누는데, 이는 자유도와 관련되어 있다.

변수가 얼마나 자유로운지에 해단 것으로 분산을 구할 때 표본 평균이 포함되어 있고, 이는 분산을 구하는 시점에는 이미 표본 평균은 정해져 있다는 것이다. 

따라서 분산을 구하는 시점에서 데이터가 n개 있다고 가정했을 때 자유롭게 정할 수 있는 데이터는 n-1 개뿐이다. 

이것이 자유도의 개념이고 분산을 구할 때 n-1 로 나누는 이유다

분산이 작은 경우에는 데이터가 밀집된 영역에 분포, 큰 경우는 넓은 영역에 퍼져 있음 이렇게 데이터의 흩어짐 정도를 정하는 파라미터를 스케일파라미터라고 부른다.

표준편차는 분산의 양의 제곱근으로 의미 파악을 위해 사용된다.

평균과 분산의 성질

평균과 분산의 성질은 다음과 같다. 먼저 서로 독립인 확률 변수의 합에 대한 기댓값이다.

증명 과정으론

기댓값에는 아래와 같은 성질도 있다. 아래 성질에서 a, c 는 상수이다.

 

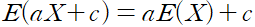
다음은 분산에 대한 성질로 서로 독립인 확률 변수의 합에 대한 분산이다.

위 성질의 증명

분산에는 아래의 성질이 있다. a, c는 상수이다.

 

상관관계

공분산

공분산 covariance 은 두 확률 변수의 상관관계를 나타내는 값이다. 만약 두 개의 확률 변수 중 하나의 값이 증가할 때 다른 값도 증가하는 경향이 있다면 공분산은 양수가 된다. 반대의 경우 음수가 된다.

공분산은 아래와 같이 정의한다.

공분산은 변수 X의 편차와 변수 Y 의 편차를 곱한 값의 평균이다.

 

공분산은 아래와 같은 식으로도 구할 수 있다.

확률 변수 X와 Y가 서로 독립일 때, 둘은 상관관계가 존재하지 않는다. 즉 공분산은 0이다.

 

위와 같이 변수 X끼리의 공분산은 변수 X의 분산과 같다.

위 성질은 공분산은 변수 순서와 상관없이 같은 값을 가진다는 의미이다.

 

위 성질은 확률 변수에 상수 a,b 를 곱했을 경우 공분산이 가지는 성질이다.

위 정리를 일반화시키면 아래와 같이 된다.

 

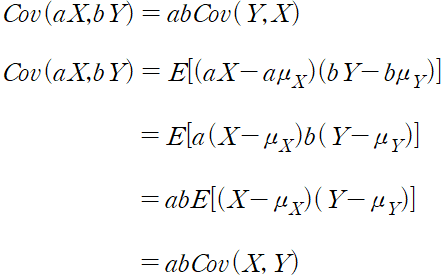
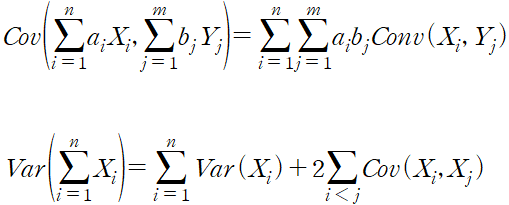
두 번째 식을 증명하면 다음과 같다.

 

확률 변수 X가 서로 독립이면 아래 식을 만족한다.

 

공분산 행렬 covariance matrix 에 대해 알아본다. 공분산 행렬은 변수 간 분산, 공분산을 행렬로 표현한 것이다. 이는 차원 축소에 자주 사용된다.

예를 들어 피처 데이터셋을 p개의 특성을 가진 n개의 데이터 포인트를 가진다.

i번째 특성의 평균을 x_i 라고 하고, 평균 행렬과 편차 행렬을 구하면 다음과 같다.

위 식에서 편차 행렬의 제곱을 구하면 다음과 같고 이를 공분산 행렬, 시그마로 표현한다.

상관 계수

공분산을 이용하면 변수 간 상관관계를 알 수 있지만 변수 간 단위가 서로 다른 경우 비교가 어렵다.

이를 보완하기 위한 개념이 상관 계수이다. 상관 계수는 공분산을 각 변수의 표준 편차로 나눔으로써 쉽게 구할 수 있다.

다음 식은 모집단 상관 계수를 의미한다.

표본 상관 계수는 아래와 같다.

 

표본 상관 계수를 계산하기 편한 식으로 구할 수 있다.

첫 번째 식의 증명

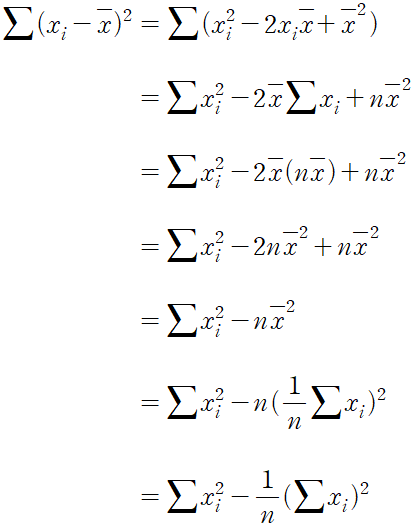
균일 분포

균일 분포 uniform distribution 은 특정 범위 내에서 확률 분포가 균일한 분포를 의미한다. 균일 분포의 경우 이산형 분포가 될 수도 있고 연속형 분포가 될 수도 있다.

이산형 균일 분포의 확률 밀도 함수와 평균, 분산은 아래와 같다. X~U(1,N) 은 확률 변수 X는 1부터 N까지 범위에서 균일 분포를 따른다는 뜻이다.

 

연속형 균일 분포는 이산형 균일 분포와는 다르게 확률 변수의 범위가 연속형이다. 

연속형 균일 분포의 확률 밀도 함수 probability density function, 평균, 분산은 아래와 같다.

균일 분포는 머신러닝에서 베이지안 방법론을 사용할 때 사전 정보가 없는 경우 초기 분포로 많이 사용된다.

 

정규 분포

normal distibution, 가우시안 분포 Gaussian distibution 라고도 한다.

다음 식은 평균이 u이고 분산이 a^2 인 정규 분포를 따른다.

 

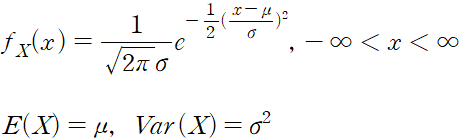
위 정규 분포 밀도 함수의 우변에서 주목해야 할 부분은 (x-u)/a 부분이다. 이 부분은 머신러닝에서의 데이터 표준화와 일치한다.

표준 정규 분포 standard normal distribution 란 평균이 0, 분산이 1 인 정규 분포를 의미한다. 

 

이항 분포

베르누이 분포

이항 분포에 앞서 베르누이 분포, 이항 분포는 베르누이 시행을 일반화한 분포, 이는 한 가지 실험에서 겱과가 오직 2개인 시행을 의미한다. 

베르누이 분포의 확률 밀도 함수, 평균과 분산은 아래와 같다.

 

확률 변수는 오직 0, 1 의 값을 가지며, 확률 변수 x가 0이라면 1-p 값을 가지며 x가 1이라면 p 값을 가진다.

이항 분포

이항 분포 binomial distribution 은 성공 확률이 p인 독립적인 베르누이 시행을 n회 했을 때 성공 횟수 X가 따르는 이산형 확률 분포, 

즉, 베르누이 시행을 n번 한 것

이항 분포의 파라미터는 시행 횟수 n과 성공 확률 p이다. 

조합을 의미하는데 n개 중 x개를 순서 성관없이 뽑을 우 있는 경우의 수

 

다항 분포

다항 분포 multinomial distribution 은 이항 분포를 일반화한 분포, 이항 분포에서는 한 번의 시행에서 나올 수 있는 결과가 오직 2개, 이를 확장한 다항 분포에서는 각 시행에서 나올 수 있는 결과가 m개로 확장된다.

결괏값으로 m개가 나올 수 있는 시행을 n번 했을 때 확률 변수 X를 다항 분포를 따른다고 하며, 각 m개의 결괏값이 나올 수 있는 확률을 p1,p2,...,pn 이다. 

다음은 다항 분포의 확률 밀도 함수이다.

 

 

최대 가능도 추정

가장 그럴듯한 추정

확률 분포에서 파라미터가 고정되어 있을 때, 샘플을 얻을 수 있는 확률을 가능도, 우도(likelihood) 라고 표기한다. 

특정 확률 분포가 주어져 있을 때 표본은 여러 번 수집이 가능하다. 그리고 매번 수집된 데이터는 같을 수도 있고 다를 수도 있다. 

즉 가능도란 파라미터가 주어질 때 해당 표본이 수집될 확률을 의미한다. 가능도를 나타내는 함수를 가능도 함수라고 한다.

확률 변수의 확률 밀도 함수를 표현

위 식은 결합 확률 밀도 함수, 위 함수를 확률 변수의 함수가 아닌 파라미터의 함수로 볼 때 이를 가능도 함수라고 한다.

argmax 부분은 식을 최대화 시키는 세타 값이다. 가능도 함수에 로그를 취함 함수를 로그 가능도 함수라고 부른다.

가능도 함수에 로그를 취할 수 있는 이유는 로그 함수가 1대 1 함수이기 때문이다 그 성질이 변하지 않는다. 

가능도 함수에서는 다수의 확률을 곱하는 형태를 띈다. 확률을 많이 곱하면 0에 수렴하므로 계산상의 오류가 발생할 가능성이 있다. 이러한 문젤르 핵려학 ㅣ위해 로그를 씌운다.

파라미터를 추정하는 데 가능도 함수가 사용된다. 가능도 함수를 사용해 가장 그럴듯한 추정값을 파라미터로 추정하는 것, 이를 최대 간으도 추정량이라고 한다. Maximum Likelihood Estimator

 

최대 사후 추정

조건부 확률

conditional probabilty 는 조건이 주어질 때의 확률, 

두 사건이 동시에 발생할 확률을 의미한다. 

교집합 형태의 확률이 주어질 경우 조건부 확률 형식으로 변형할 수 있다. 두 사건이 독립이면 P(A)P(B) 와 같이 표현 가능

베이즈 추정

베이지안은 파라미터를 확률 변수로 보는 방법이다. 

파라미터가 확률 변수이므로 해당 파라미터의 확률을 구할 수 있다. 이때, 사건이 발생하기 전 파라미터의 확률인 P(a)를 사전 확률 밀도 함수라고 한다. 파라미터와 표본x 가 동시에 얻어질 확률을 다음과 같이 구할 수 있다.