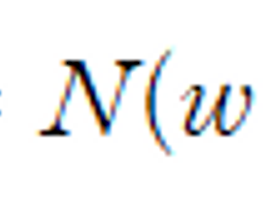라그랑주 승수법을 이용하여
정규화된 오류 함수를 최소화하는 것이
정규화되지 않은 곱합 오류를 제약 조건하에서 최소화하는 것과 동일하다는 것의 증명
n, lambda 의 관계에 대해 논하라
정규화된 오류 함수
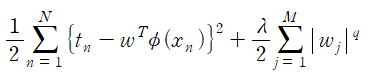
정규화 되지 않은 곱합 오류
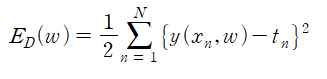
제약 조건

제약 조건의 재작성

편의상 1/2 의 도입(deliberately)
라그랑주 함수 사용

해당 식과 정규화된 오류 함수 를 정규화되지 않은 곱합 오류를 제약조건 하에서 최소화하는 것과 동일,
w 에 대해 동일한 의존성을 갖는 것이 명백하다.
한편 L(w,lambda) 를 최소화할 수 있는 최적 w 를 w*(lambda) 로 표시하면,

해당 식을 얻는다.
라그랑주 식의 최소화.
근데 그럼 n 은 뭔데 제약 조건식의 형태 때문에 생긴건가.

n 과 lambda 사이의 관계 파악,
위의 식에서는 단순히 라그랑주 함수의 2번째 항을 0으로 만드는 n 값,

0 보다 큰 lambda 값에 대해서 정규화 오류 함수의 최소화, w 에 대한 값을 w*(h) 로 나타내고 KKY 를 사용하면 n 값을 얻을 수 있다.
이러한 내용의 기저가 되는 내용,
정규화 오류 함수에서 q = 1 인 경우를 라쏘 lasso 라 한다. 이 때 lambda 값을 충분히 크게 설정하면 몇몇 계수 w 가 0이 된다. 이러한 모델을 희박한 모델( 많은 가중치가 0 인 경우 ) 이라고 한다.
이때 계수가 0이 된 해당 항의 기저 함수는 더 이상 사용되지 않는다. ?? 먼말알?
정규화의 경우 최적의 모델 복잡도 탐색 문제에서 적절한 정규화 계수 lambda 를 찾는 문제로 변경
라그랑주 승수법
undermined multiplier, lagrange multiplier 는 하나 이상의 제약 조건하에서 여러 변수에 대한 함수의 임계점을 찾는 데 사용,
D 차원 변수 x 에서 제약 조건 g(x) = 0 은 x 공간상의 D-1 차원 표면에 해당한다. ( 함숫값이 0이니까!!! )
제약 조건 표면상(g(x) = 0)의 모든 포인트들에 대해서 제약 조건 함수에 대한 기울기 d g(x) 들은 표면에 대해 직교할 것이다.( 왜??)
이를 확인하기 위해 제약 조건 표면상의 포인트 x 와 x+e 의 고려 (둘 다 제약 조건 표면상의 포인트)
x 주변에 대해 테일러 전개를 시행하면
g(x+e) ~= g(x) + e^T d g(x)
을 얻게 된다. (그치 이거까진 맞지)
x 와 x + e 는 둘 다 제약 조건 평면상 위치, g(x) = g(x+e), e^T d g(x) 의 값이 0과 비슷할 것,
lim(e) -> 0 일수록 e^T d g(x) 는 0이 된다.
이것은 벡터 e 가 제약 조건 평면 에 대해 평행하다는 것, 해당 값이 0이 되기 위해서는 d g 는 표면에 대해 수직이어야 한다.
다음으로는 f(x) 가 최대화되는 결정 표면상의 x* 를 찾아야 한다.
이러한 포인트는 d f(x) 가 제약 조건 평면에 대해 직교하는 성질을 가져야 한다. - 이건 또 왜??
이 경우 제약 조건 표면을 따라 짧은 거리를 이동시킴으로써 f(x) 의 값을 더 증가 시킬 수 있기 때문 - 아하 작은 변화로 더 많은 증가를 얻을 수 있기에...
제약 조건 평면은 g(x) = 0 을 이루는 평면임을 계속 인지....
df 와 dg 는 평행한 벡터이어야 하므로, df + lambda dg = 0 을 만족하는 매개변수 lambda 가 존재할 것,
0이 아닌 lambda 를 라그랑주 승수 lagrange multiplier 라 한다.
다음으로 정의된 라그랑주 함수 도입
L(x, lambda) ≡ f(x) + lambda g(x)
제약된 정류 조건은 d L_x = 0 으로 설정함으로써 구할 수 있다.
또한 조건 d L / d lambda = 0 에 따라 제약 조건식 g(x) = 0 을 얻게 된다.
(람다 변화량에 대한 라그랑주 함수 변화량이 0이면 g(x) = 0 을 얻네 ㅇㅇ)
따라서 제약조건 g(x) = 0 하에서 함수 f(x) 의 최댓값을 얻기 위해서는 라그랑주 함수를 정의하고 x 와 lambda 에 대한 L(x, lambda) 의 임계점을 찾아야 한다.