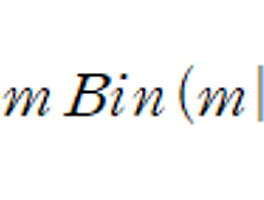제곱식의 완성 테크닉을 이용해서 선형 기저 함수 모델의 매개변수 w 의 사후 분포에 대한 식

의 결과를 증명하라.
이때 m_N 과 S_N 은 다음의 식에 따라 정의된다.

wirting down the prior distribution p(w) and likelihood function p(t|X,w,beta)

노이즈 정밀도 매개변수 beta 가 알려져 있는 상수라고 가정, 결정함수 y(x,w) 와 가우시안 노이즈 합으로 주어진 타깃 변수 t, t = y(x,w) + e
e 는 0을 평균, beta 를 정밀도로 가지는 가우시안 확률 변수

제곱 오류 함수를 가정할 경우 새 변수 x 에 대한 최적의 예측값은 타깃 변수의 조건부 평균으로 주어질 것이다. 위 식의 형태에 가우시안 조건부 분포의 경우에 조건부 평균

Since the posterior Probability Density Function equals to the product of the prior PDF and likelihood function, up to a normalizaed constant. We mainly focus on the exponential term of the product

Hence, by ccomparing the quadratic term with standard Gaussian Distribution, we can obtain
S_N^-1 = S_0^-1 + beta PHI^T PHI.
and then comparing the linear term,
we can obtain: