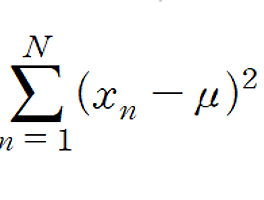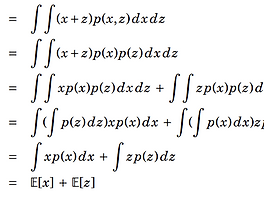pattern recognition and machine learning 1-9, 가우시안 분포의 최댓값, mu ( 단변량, 다변량 ) x 에 대한 미분을 통해 증명

가우시안 분포식의 최빈ㄱ밧이 mu 로 주어짐을 증명, 

다변량 가우시안 분포의 최빈값이 mu 임을 증명

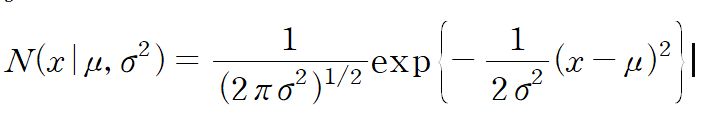
미분을 통해 확인 가능,

setting this to zero we obtain x = mu

 

다변량도 동일하게 미분 수행, 

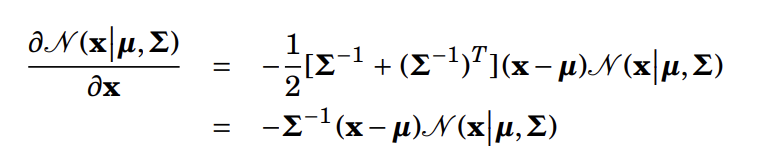
Where we take advantage of 

 

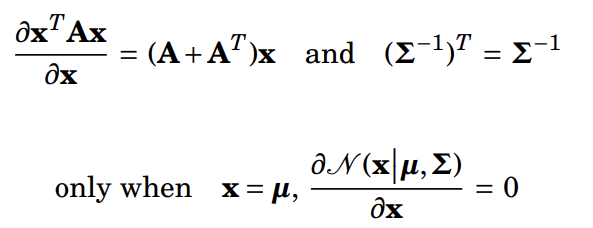
You may also need to calculate Hessian Matrix to prove that it is maximum. However, here we find that the first derivative only has one root. 

Based on the description in the problem, this point should be maximum point