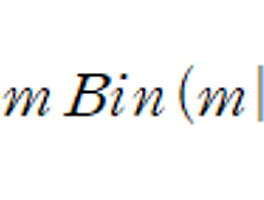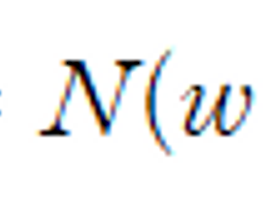다변량 타깃 변수 t 에 대한 선형 기저 함수 회귀 모델의 고려,
타깃 변수가 다음의 가우시안 분포를 가진다.

입력 기저 벡터 phi(x_n) 과 해당 타깃 변수 t_n 으로 이루어진 훈련 집합도 가정
이때 매개변수 행렬 W 의 최대 가능도 해 W_ML 은 각각의 열이

정규 방정식의 형태로 주어지는 성질을 가진다는 것을 증명하라.
정규 방정식은 등방 노이즈 분포에 대한 해, 이 해와 공분산 행렬 SIGMA 는 독립적이라는 점을 주목
SIGMA 행렬은 공분산 행렬, 입력 데이터
D 차원 벡터 x, SIGMA 는 D × D 공분산 행렬, 대각 행렬 ( x 가 D 차원 벡터고 공분산이 x 값들에 대한 연산 이므로)
log likelihood function 의 작성,

다변량 가우시안 분포의 log likelihood,
w 에 대한 미분값의 0 설정

정규 방정식을 통한 다음의 식 획득
위 식의 전개로 다음의 정규 방정식 형태를 얻을 수 있고,

설계 행렬에 대한 이해 필요 ( phi(x) @ phi(x) ) 라는 것을 알겠음,
최대 가능도 해에 대해 풀

SIGMA 의 최대 가능도 해
위 식에 대한 해석이
as required. Since we are finding a joint maximum with respect to both W and Σ we see that it is WML which appears in this expression, as in the standard result for an unconditional Gaussian distribution.
... 어렵넹..