이는 양자역학이 고전역학과 근본적으로 다른 세 가지 구조적 특성을 가지기 때문,
✅ 요약 대답 먼저
양자역학에서는 관측 가능한 물리량들이 연산자(operator) 로 표현되는 이유는:
- 측정은 상태를 바꾸는 행위이기 때문이고
- **불확정성 원리(비가환성)**을 반영하기 위해서이며
- **상태가 함수(혹은 벡터)**이기 때문에,
그 위에 작용하는 물리량은 함수를 변형하는 연산자가 되어야 합니다.
✅ 1. 상태가 벡터이기 때문 → 물리량은 함수에 작용하는 것
양자계의 상태는 psi(x) 라는 함수 또는 힐베르트 공간의 벡터
관측 가능한 물리량은 이 상태에 작용해서 새로운 상태를 만들어 낸다.
-> 즉, 함수를 입력 받아 함수를 반환하는 것 = 연산자
양자역학에서는 입자가 퍼져 있는 상태 -> 수치가 아닌 분포이므로, 그 위에서 의미를 가지는 것은 숫자 평가가 아닌 작용!
✅ 2. 연산자의 비가환성 (non-commutativity): 양자의 핵심 구조
물리량들이 함수가 아닌 함수 사이의 변환자가 되어야만 양자계의 본질적인 특성 ( 동시측정 불가, 중첩, 간섭 등 ) 을 수학적으로 담을 수 있다.
비가환 연산자 non-commuting operators
1. 비가환 연산자 정의
두 연산자 A^, B^ 에 대해 :
[A^, B^] = A^B^ - B^A^
를 교환자 commutator 라고 한다.
[A^, B^] = 0 가환, [A^, B^] != 0 비가환
2. 유명한 예 : 위치와 운동량
양자역학의 대표적인 비가환 연산자 : [x^, p^] = i h
x^ : 위치 연산자
p^ : 운동량 연산자

파동 함수, psi(x) 위에 작용하는 연산자는 다음과 같다.
위치 연산자 : 단순히 위치 변수, x 를 곱함
운동량 연산자 : 파동함수를 x 에 대해 미분하고 상수를 곱함

(편미분 생각하기)
둘의 차이 계산 : 교환자
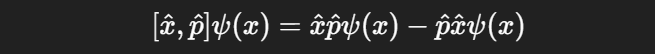

✅ 3. 비가환성의 물리적 의미
1. 동시에 정확히 측정 불가
위치와 운동량은 정확히 동시에 측정할 수 없음 -> 하이젠베르크 불확정성 원리

공통 구유 상태가 존재하지 않음
✅ 3. 측정이 단순한 평가가 아니라 작용이기 때문에
고전역학에서의 관측 - > 측정 = 값 읽기
양자역학에서의 관측 : 측정은 상태를 바꾸는 행위
- 상태가 고유값 상태이면 측정 결과는 확정
- 아니면 측정 결과는 확률적으로 튀며, 상태는 측정 후 고유 상태로 붕괴
물리량은 상태를 바꾸는 작용을 수반하며, 이 작용은 수학적으로 연산자 형태로 나타나야 한다.
✅ 4. 에르미트 연산자(Hermitian Operator): 실수 고유값을 보장
관측 가능한 물리량은 항상 real 값이어야 한다.
이를 보장하기위해, 양자 역학의 물리량 연산자들은 반드시 Hermitian 여야 한다.
Hermitian 연산자의 고유값은 실수이고, 고유 벡터는 직교 - > 확률 해석과 직결
정리하자면, 확률 밀도에 대한 해석으로서, 특정한 값을 원하는게 아니므로, 연산자 형태로 표현될 수 밖에 없었네특성을 가지기 때문,
✅ 요약 대답 먼저
양자역학에서는 관측 가능한 물리량들이 연산자(operator) 로 표현되는 이유는:
측정은 상태를 바꾸는 행위이기 때문이고
**불확정성 원리(비가환성)**을 반영하기 위해서이며
**상태가 함수(혹은 벡터)**이기 때문에,
그 위에 작용하는 물리량은 함수를 변형하는 연산자가 되어야 합니다.
✅ 1. 상태가 벡터이기 때문 → 물리량은 함수에 작용하는 것
양자계의 상태는 psi(x) 라는 함수 또는 힐베르트 공간의 벡터
관측 가능한 물리량은 이 상태에 작용해서 새로운 상태를 만들어 낸다.
-> 즉, 함수를 입력 받아 함수를 반환하는 것 = 연산자
양자역학에서는 입자가 퍼져 있는 상태 -> 수치가 아닌 분포이므로, 그 위에서 의미를 가지는 것은 숫자 평가가 아닌 작용!
✅ 2. 연산자의 비가환성 (non-commutativity): 양자의 핵심 구조
물리량들이 함수가 아닌 함수 사이의 변환자가 되어야만 양자계의 본질적인 특성 ( 동시측정 불가, 중첩, 간섭 등 ) 을 수학적으로 담을 수 있다.
비가환 연산자 non-commuting operators
1. 비가환 연산자 정의
두 연산자 A^, B^ 에 대해 :
[A^, B^] = A^B^ - B^A^
를 교환자 commutator 라고 한다.
[A^, B^] = 0 가환, [A^, B^] != 0 비가환
2. 유명한 예 : 위치와 운동량
양자역학의 대표적인 비가환 연산자 : [x^, p^] = i h
x^ : 위치 연산자
p^ : 운동량 연산자

파동 함수, psi(x) 위에 작용하는 연산자는 다음과 같다.
위치 연산자 : 단순히 위치 변수, x 를 곱함
운동량 연산자 : 파동함수를 x 에 대해 미분하고 상수를 곱함

(편미분 생각하기)
둘의 차이 계산 : 교환자


✅ 3. 비가환성의 물리적 의미
1. 동시에 정확히 측정 불가
위치와 운동량은 정확히 동시에 측정할 수 없음 -> 하이젠베르크 불확정성 원리

공통 구유 상태가 존재하지 않음
✅ 3. 측정이 단순한 평가가 아니라 작용이기 때문에
고전역학에서의 관측 - > 측정 = 값 읽기
양자역학에서의 관측 : 측정은 상태를 바꾸는 행위
상태가 고유값 상태이면 측정 결과는 확정
아니면 측정 결과는 확률적으로 튀며, 상태는 측정 후 고유 상태로 붕괴
물리량은 상태를 바꾸는 작용을 수반하며, 이 작용은 수학적으로 연산자 형태로 나타나야 한다.
✅ 4. 에르미트 연산자(Hermitian Operator): 실수 고유값을 보장
관측 가능한 물리량은 항상 real 값이어야 한다.
이를 보장하기위해, 양자 역학의 물리량 연산자들은 반드시 Hermitian 여야 한다.
Hermitian 연산자의 고유값은 실수이고, 고유 벡터는 직교 - > 확률 해석과 직결
정리하자면, 확률 밀도에 대한 해석으로서, 특정한 값을 원하는게 아니므로, 연산자 형태로 표현될 수 밖에 없었네
gpt 추가 답변 :
보충 1 : 측정은 상태에 작용하는 행위
확률 밀도라는 해석은 측정 결과가 확정된 수치가 아니라 분포다 라는 점에서 맞지만, 양자역학에서 측정은 단순히 수를 추출하는 행위가 아니다.
측정이란 연산자 A^ 가 상태 | PSI > 에 작용하여, 고유값을 얻고 상태를 고유벡터로 붕괴 collapse 시키는 일종의 변형 과정
즉, 물리량이 연산자인 이유는, 그 결과를 얻기 위해 상태에 특정 연산을 '적용' 해야 하기 때문
보충 2 : 물리량 간의 구조 ( 비가환성 ) 을 담기 위해
확률 해석을 수용한다면, 여러 물리량 간의 관계도 확률적으로 해석되어야 한다.
단순 값의 경우 비가환 구조를 만들 수 없다. = > 그래서 물리량을 연산자로 추상화하여 물리적 제약을 수학에 담는다.
보충 3 : 기댓값이 내적 구조로 표현되기 때문
기댓값은 단순히 실수 함수 곱으로 표현되지 않는다.

대부분의 물리량은 미분을 포함하거나 복잡한 작용을 하므로

이때 연산자 A^ 가 함수에 작용해야 기댓값을 계산할 수 있다.
확률 밀도 해석만으로는 이 작용 구조를 포괄하지 못하고 기댓값 구조 자체가 연산자 형태를 강제한다.
보충 4 : 결과값 자체도 확률적이지만 그 결과를 만드는 과정도 구조적이다.
양자에서는 위치, 운동량 각각에 대한 측정 절차가 존재하고, 그 순서에 따라 다른 결과가 나오며, 그 전체 구조가 연산자 수학으로 표현된다.
보완 포인트설명
| ✅ 상태에 “작용하는” 구조 | 단순 값이 아닌 작용(변형) 과정 |
| ✅ 비가환 구조 수용 | 여러 물리량의 관계를 표현하려면 연산자 구조 필수 |
| ✅ 기댓값이 연산자 내적 구조 | 단순 ( A(x) |
| ✅ 관측 행위가 물리적 작용 | 측정이 곧 상태 변화 → 함수 작용자 필요 |
'양자역학' 카테고리의 다른 글
| 양자역학에서의 expectation value, 내적이 왜 기댓값이 되는지?? 그리고 내적에 대해 (0) | 2025.05.09 |
|---|---|
| 운동량 (0) | 2025.05.09 |
| 파동 함수의 normalization condition, 확률적 해석을 위해 임의로 만든 방정식이네... (0) | 2025.05.09 |
| 드보르이의 등장( 전자는 파동이다-전자의 각 운동과, 전자의 운동량을 통해) (2) | 2023.01.03 |
| 양자역학의 등장 배경 (빛은 파동에서부터 하이젠베르크까지) (0) | 2023.01.03 |



