PSI 상태 : 양자계의 상태를 나타내는 힐베르트 공간 벡터
psi(x) : 위치 표현에서의 파동함수
PSI 상태에 있는 입자에 대한 x 의 기댓값
Expectation value, 기댓값
<x> 은 psi 상태에서 입자의 평균 위치를 의미한다. 이는 실험적으로 같은 상태를 여러 번 반복 측정했을 때 얻어지는 평균값
수학적 정의 (파동함수 표현)
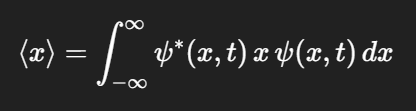
파동 함수의 중심이자, 움직임을 추적할 수 있는 평균 위치
시간에 따라 <x(t)> 이 어떻게 변하는지는 운동 방정식에 해당
양자역학에서는 관측 가능한 물리량 ( 관측량, observable) 들은 모두 연산자 operator 로 표현된다. 그리고 그 물리량의 기댓값 expecttation value 는 다음과 같이 계산된다.
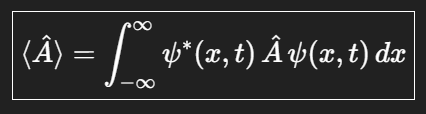
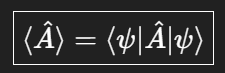
왜 연산자를 사이에 끼워넣는 방식인가??
기댓값 = 평균값 - 확률 가중 평균
확률 밀도 : |psi(x)|^2 = psi*(x) psi(x)

고전 역학에서, 위치 운동량, 에너지 등은 숫자 함수로, 단순한 값임
양자역학에서는
관측 가능한 물리량은 연산자로 표현된다.
고전역학에서의 기댓값,
입자가 위치 x 에 있을 확률 밀도가 p(x) 라면, 물리량 A(x) 의 평균은

p(x) 는 항상 실수 확률 밀도이므로 곱해서 적분하면 됨
양자역학에서는 상태가 복소수 : PSI(x)

문제는 운동량 같은 연산이 단순한 곱셈이 아니라 연산자라는 점
운동량 연산자는 다음과 같이 미분 연산자이다.

즉, 이건 단순히 어떤 값과 곱하는 게 아니라, 함수 phi(x) 에 작용해서 다른 함수로 바꾸는 연산자
연산자는 phi 에 작용해서 새로운 함수를 만들고, 그 결과를 phi* 과 내적해야 기댓값을 의미 있게 정의할 수 있다.
기댓값은 내적으로 정의됨 ( 힐베르트 공간 관점 )
양자역학에서는 상태 |phi> 가 힐베르트 공간의 벡터이기 때문에, 기댓값은 벡터 사이의 내적 형태로 표현해야만 한다.
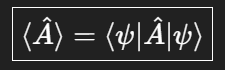
직관적으로 보면
- A^ | phi > : phi 상태에 연산자 A^ 가 작용해 새로운 상태 벡터 생성
- <phi | : 원래 상태의 복소수 켤레
- 그 둘의 내적 -> 원래 상태와 연산된 상태의 유사도 -> 기댓값
왜 끼워 넣는가? : 연산자는 phi 를 작동시켜 다른 함수로 만들고 그걸 원래 상태 phi* 와 내적해서 평균을 구한다.
'양자역학' 카테고리의 다른 글
| 시간에 무관한 슈뢰딩거 방정식, 퍼텐셜 V(x) 가 왜 time independent 라고 가정하는지 (0) | 2025.05.09 |
|---|---|
| 양자역학에서의 expectation value, 내적이 왜 기댓값이 되는지?? 그리고 내적에 대해 (0) | 2025.05.09 |
| 양자 역학에서는 물리량이 왜 단순 숫자 함수가 아닌 연산자의 형태를 띄는가? (0) | 2025.05.09 |
| 파동 함수의 normalization condition, 확률적 해석을 위해 임의로 만든 방정식이네... (0) | 2025.05.09 |
| 드보르이의 등장( 전자는 파동이다-전자의 각 운동과, 전자의 운동량을 통해) (2) | 2023.01.03 |



