박테리아 배양실험에서 박테리아 수 N 은 시간 t 의 함수이므로 N = f(t) 로 나타낼 수 있다.
관점을 바꿔 개체 수가 일정 수준에 도달하는 시간을 구하려고 한다고 생각해본다.
이러한 함수를 f 의 역함수라고 부르고 f^-1 로 나타내며, f 의 역이라고 읽는다.
t = f^-1(N) 은 개체 수가 N 에 도달하기 위해 필요한 시간이다.
모든 함수가 역함수를 갖는 것은 아니다.

이러한 성질을 갖는 함수를 일대일 함수라고 부른다.
만약 함수 f 가 같은 값을 두 번 이상 취하지 않는다면 일대일함수라고 부른다.
만약 어떤 수평션이 f 의 그래프와 두 점 이상에서 만난다면 f(x_1) = f(x_2) 를 만족하는 수 x_1 과 x_2 가 존재함을 알 수 있다.
수평선 판정법
함수가 일대일이 될 때 필요충분조건은 그래프가 모든 수평선과 두 번 이상 만나지 않는 것이다.
일대일함수는 다음 정의에 따라 역함수를 갖는 함수이기 때문에 중요하다.
정의
f 는 정의역 A 와 치역 B 를 갖는 일대일함수라 하자. 그러면 f 의 역함수 f^-1 는 정의역 B 와 치역 A 를 가지며 B의 임의의 y 에 대하여 아래와 같이 정의된다.

로그함수
b > 0 이고 b != 1 이면 지수함수 f(x) = b^x 는 증가하거나 감소하고 수평선 검사에 의해 일대일함수이다.
그러므로 이것은 log_b 로 나타내면서 밑 b 를 가지는 로그함수로 불리는 역함수 f^-1 를 가진다.

자연로그
로그의 모든 가능한 밑 b 중에서 e 를 선택하는 것이 가장 편리하다는 것을 알 수 있다.
밑이 e 인 로그는 자연로그라고 부르고
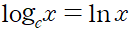
라는 기호로 나타낸다.
역삼각함수
역삼각함수를 구하기는 쉽지 않은데, 그 이유는 삼각함수는 일대일함수가 아니므로 역함수를 갖지 않기 때문이다. 그러나 함수들이 일대일함수가 되도록 정의역을 제한하여 이 문제를 해결할 수 있다.
사인함수는 일대일이 아니지만, 함수 f(x) = sin x, -pi/2 <= x <= pi/2 는 일대일이다.
정의역이 제한된 사인함수 f 의 역함수는 존재하고 sin^-1 또는 arcsin 으로 나타낸다.

'미적분 > 미분적분학' 카테고리의 다른 글
| 2.2 함수의 극한 (0) | 2022.12.21 |
|---|---|
| 2.1 접선과 속도 문제 (0) | 2022.12.21 |
| 1.4 지수함수 (0) | 2022.12.21 |
| 1.3 알고 있는 함수에서 새 함수로 (0) | 2022.12.21 |
| 1.2 수학적 모델 (0) | 2022.12.21 |



