2.1 접선과 속도 문제

접선 문제

곡선의 접선은 곡선과 접하는 직선이다. 즉, 접선은 접점에서 곡선과 같은 방향을 가져야 한다. 

유클리드의 정의에 따라 원에서 접선은 단순히 그 원과 오직 한 점에서 만나는 직선이라 할 수 있다. 

포물선 y = x^2 의 접선 t 를 구하는 예제를 본다.

예제 점 P(1,1) 에서 포물선 y = x^2 의 접선의 방정식을 구하여라

접선 t 의 기울기 m 을 구하면 접선의 방정식을 구할 수 있을 것이다. 기울기를 구하기 위해서는 두 점이 필요하지만, t 위의 오직 한 점 P 만을 알고 있어서 어려움이 있다.

포물선 위의 가까운 점 Q(x,x^2) 를 잡고 할선 PQ 의 기울기 m_PQ 를 구하여 m 의 근삿값을 구할 수 있음을 알 수 있다. 

예를 들어 점 Q (1.5, 2.25) 에 대하여, m_PQ = 2.5

Q 가 P 에 가까워질수록 x 는 1과 가까워지고, m_PQ 는 2에 가까워진다. 이는 접선 t 의 기울기가 m=2 임을 암시한다.

접선의 기울기가 2라면 직선의 방정식의 점-기울기 형태를 사용하여 (1, 1) 을 지나는 접선의 방정식을 구할 수 있다.

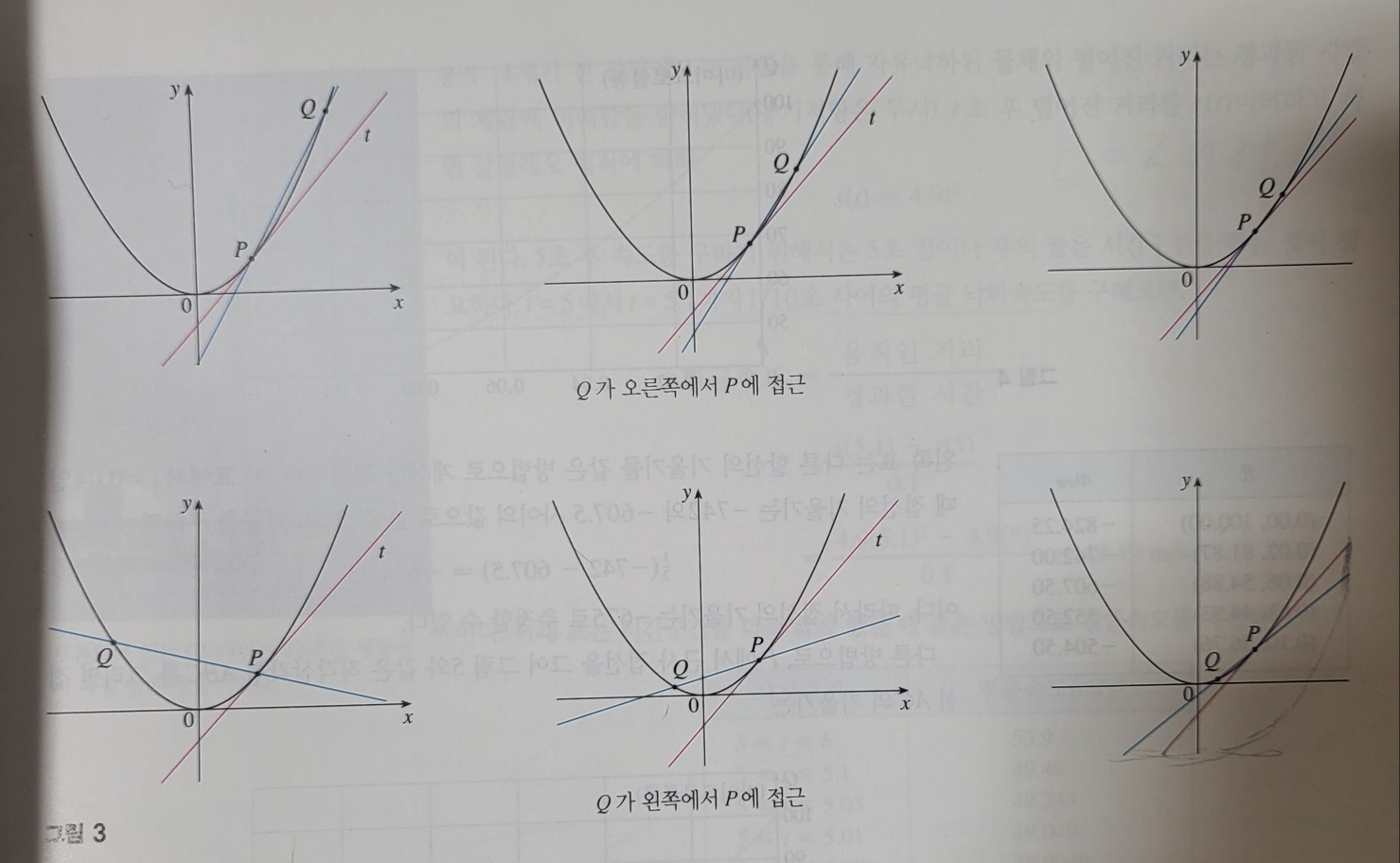
Q 가 포물선을 따라 P 에 가까워질 때 대응하는 할선은 P 를 중심으로 회전하면서 접선 t 에 접근한다.

과학에서 나타나는 많은 함수들은 명확한 식으로 나타나지는 않는다. 그들은 실험 데이터에 의해 정의된다. 

속도 문제

속도계를 보고 차가 각 순간에 일정한 속도를 가지고 있다고 가정하지만, 순간적인 속도는 어떻게 정의하는가? 낙하하는 공의 예제를 살펴본다.

예제

토론토에 있는 지상 450m 높이의 타워 전망대에서 공을 떨어뜨릴 때 5초 후의 공의 속도를 구하여라.

5초 후 속도를 구하기 위해서는 5초 전이나 후의 짧은 시간구간을 잡는 것이 필요하다. 

t = 5 에서 t = 5.1 까지 1/10 초 사이의 평균 낙하속도를 구해보면, 49.49m/s 이다. 

시간구간이 짧을수록 평균 속도가 49 m/s 에 가까워짐을 알 수 있다. t = 5 일때의 순간속도는 t = 5 로부터의 시간구간을 더욱더 줄여나갔을 때 평균속도의 극한으로 정의된다. 따라서 5초 후의 속도는

v = 49 m/s 이다.

예제들을 통해 알 수 있듯이 접선과 속도 문제를 해결하기 위해서는 극한을 구해야한다.