앞 절에서는 접선이나 속도를 구할 때 극한이 어떤 역항르 하는지 살펴보았다.
f(x) = x^2 - x + 2 일 때, x = 2 근방에서 함수 f 의 움직임을 조사한다.
f 의 그리프로부터 x 가 2 에서 가까워질수록 f(x) 는 4 에 가까워짐을 알 수 있다. 이것을 x 가 2 에 접근할 때 함수 f(x)=x^2-x+2 의 극한은 4 이다. 라고 말하고

정의
a 와 같지는 않지만 a 에 충분히 가까운 x 를 잡으면 L 에 얼마든지 가까운 f(x) 값을 얻을 수 있을 때

로 나타내고 x 가 a 에 접근할 때 f(x) 의 극한은 L 이다. 라고 말한다.
극한의 정의에서 x != a 라는 문구에 유의해야 한다. 이것은 x = a 를 고려하지 않겠다는 의미다. 실제로 근방에서 f 가 어떻게 정의되어 있느냐가 관심일 뿐이다.
한쪽 극한
예제
헤비사이드 Heaviside 함수 H 는
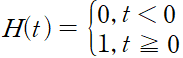
로 정의된다. 이는 시간 t=0 에서 스위치를 켤 때의 전류를 나타내는 데 사용된다.
t 가 왼쪽에서 0에 접근할 때 H(t) 는 0 에 접근한다. t 가 오른쪽에서 0 에 접근할 때 H(t) 는 1 에 접근한다. H(t) 는 하나의 값에 접근하지 않으므로 lim(H(t)) 의 값은 존재하지 않는다.
무한극한
x 가 a 에 점점 더 가까이 갈 때 f(x) 의 값이 점점 더 크게 되는 것을 기호로

로 나타낸다.
정의
f 가 a 의 양쪽에서 정의된 함수라 하자.

x 를 a 에 충분히 가깝게 잡을 때 f(x) 값을 임의로 작게 할 수 있음을 의미한다.
정의
다음 명제들 중 적어도 하나가 참이면 직선 x = 1 를 곡선 y=f(x) 의 수직 점근선이라 한다.

그래프가 수직점근선을 갖는 함수의 다른 예는 자연로그함수 y = ln x 이다. 우극한이 -INF 임을 알 수 있고, 또한 직선 x = 0 은 수직점근선이다.
'미적분 > 미분적분학' 카테고리의 다른 글
| 2.4 극한의 엄밀한 정의 (0) | 2022.12.22 |
|---|---|
| 2.3 극한법칙을 이용한 극한 계산 (0) | 2022.12.22 |
| 2.1 접선과 속도 문제 (0) | 2022.12.21 |
| 1.5 역함수와 로그 (1) | 2022.12.21 |
| 1.4 지수함수 (0) | 2022.12.21 |



