곡선은 접점 근방에서 접선과 매우 가깝게 놓여 있음을 보았다. 실제로 미분가능한 함수의 그래픠 위의 한 점 부근을 확대함으로써, 그래프가 점점 더 접선과 같아 보인다. 이 관찰은 함수의 근삿값을 구하는 방법의 근간이 된다.
함수의 값 f(a) 를 계산하는 것은 쉽지만, f 의 근삿값을 구하는 것은 어렵거나 불가능할 수도 있다. 따라서 점 (a, f(a)) 에서 f 의 접선을 그래프로 갖는 1차함수 L 의 값을 쉽게 계산할 수 있다면 문제를 해결할 수 있다.
다시 말하면, x 가 a 에 가까이 있을 때 곡선 y = f(x) 에 대한 근사식으로 점(a, f(a)) 에서의 f 의 접선을 이용한다.


접선의 방정식과 근사식을 a 에서의 f 의 선형 근사식 또는 접선 근사식이라 부른다.
이 접선을 그래프로 갖는 1차함수
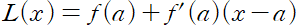
를 a 에서 f 의 선형화라고 부른다.
'미적분 > 미분적분학' 카테고리의 다른 글
| 4.1 최댓값과 최솟값 (0) | 2022.12.24 |
|---|---|
| 3.11 쌍곡선함수 (0) | 2022.12.24 |
| 3.1 다항함수와 지수함수의 도함수 (1) | 2022.12.23 |
| 2.8 함수로서 도함수 (0) | 2022.12.22 |
| 2.7 미분계수와 변화율 (0) | 2022.12.22 |


